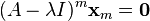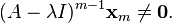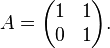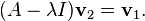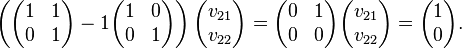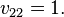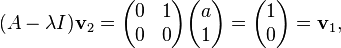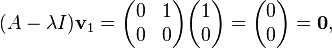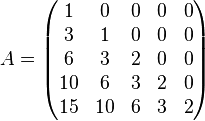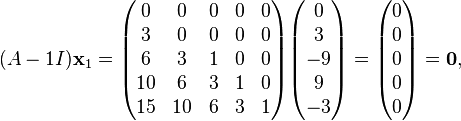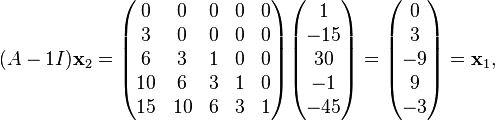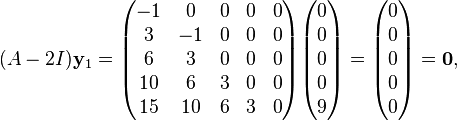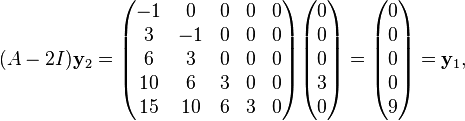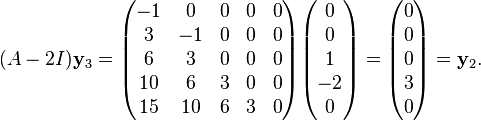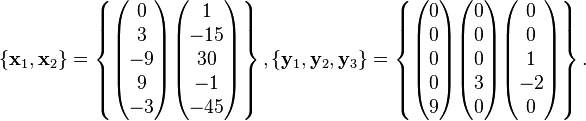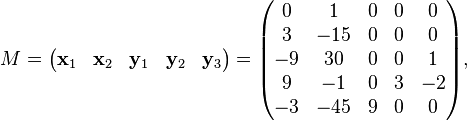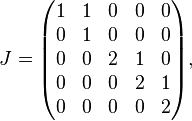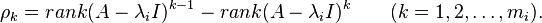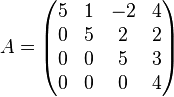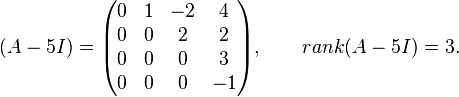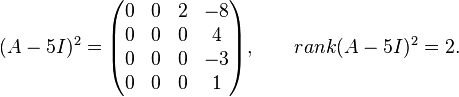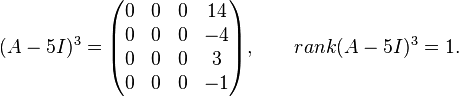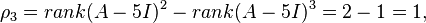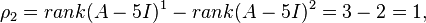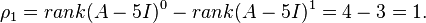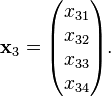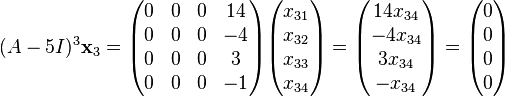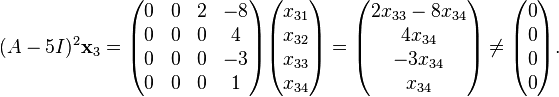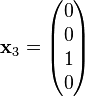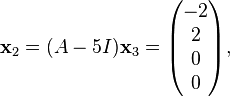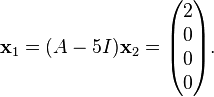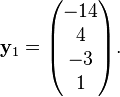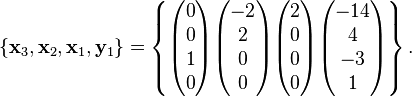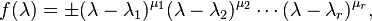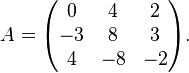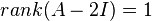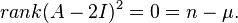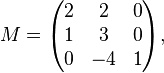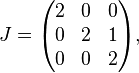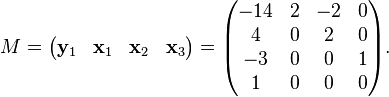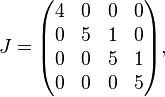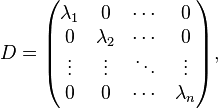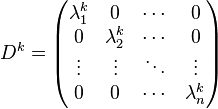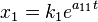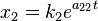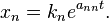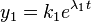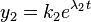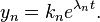Generalized eigenvector
In linear algebra, a generalized eigenvector of an n × n matrix  is a vector which satisfies certain criteria which are more relaxed than those for an (ordinary) eigenvector.[1]
is a vector which satisfies certain criteria which are more relaxed than those for an (ordinary) eigenvector.[1]
Let  be an n-dimensional vector space; let
be an n-dimensional vector space; let  be a linear map in L(V), the set of all linear maps from
be a linear map in L(V), the set of all linear maps from  into itself; and let
into itself; and let  be the matrix representation of
be the matrix representation of  with respect to some ordered basis.
with respect to some ordered basis.
There may not always exist a full set of n linearly independent eigenvectors of  that form a complete basis for
that form a complete basis for  . That is, the matrix
. That is, the matrix  may not be diagonalizable.[2][3] This happens when the algebraic multiplicity of at least one eigenvalue
may not be diagonalizable.[2][3] This happens when the algebraic multiplicity of at least one eigenvalue  is greater than its geometric multiplicity (the nullity of the matrix
is greater than its geometric multiplicity (the nullity of the matrix 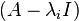 , or the dimension of its nullspace). In this case,
, or the dimension of its nullspace). In this case,  is called a defective eigenvalue and
is called a defective eigenvalue and  is called a defective matrix.[4]
is called a defective matrix.[4]
A generalized eigenvector  corresponding to
corresponding to  , together with the matrix
, together with the matrix 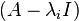 generate a Jordan chain of linearly independent generalized eigenvectors which form a basis for an invariant subspace of
generate a Jordan chain of linearly independent generalized eigenvectors which form a basis for an invariant subspace of  .[5][6][7]
.[5][6][7]
Using generalized eigenvectors, a set of linearly independent eigenvectors of  can be extended, if necessary, to a complete basis for
can be extended, if necessary, to a complete basis for  .[8] This basis can be used to determine an "almost diagonal matrix"
.[8] This basis can be used to determine an "almost diagonal matrix" 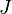 in Jordan normal form, similar to
in Jordan normal form, similar to  , which is useful in computing certain matrix functions of
, which is useful in computing certain matrix functions of  .[9] The matrix
.[9] The matrix 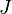 is also useful in solving the system of linear differential equations
is also useful in solving the system of linear differential equations 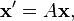 where
where  need not be diagonalizable.[10][11]
need not be diagonalizable.[10][11]
Overview and definition
There are several equivalent ways to define an ordinary eigenvector.[12][13][14][15][16][17][18][19] For our purposes, an eigenvector 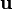 associated with an eigenvalue
associated with an eigenvalue  of an
of an  ×
×  matrix
matrix  is a nonzero vector for which
is a nonzero vector for which 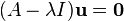 , where
, where  is the
is the  ×
×  identity matrix and
identity matrix and 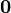 is the zero vector of length
is the zero vector of length  .[20] That is,
.[20] That is, 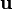 is in the kernel of the transformation
is in the kernel of the transformation 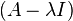 . If
. If  has
has  linearly independent eigenvectors, then
linearly independent eigenvectors, then  is similar to a diagonal matrix
is similar to a diagonal matrix  . That is, there exists an invertible matrix
. That is, there exists an invertible matrix  such that
such that  is diagonalizable through the similarity transformation
is diagonalizable through the similarity transformation 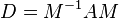 .[21][22] The matrix
.[21][22] The matrix  is called a spectral matrix for
is called a spectral matrix for  . The matrix
. The matrix  is called a modal matrix for
is called a modal matrix for  .[23] Diagonalizable matrices are of particular interest since matrix functions of them can be computed easily.[24]
.[23] Diagonalizable matrices are of particular interest since matrix functions of them can be computed easily.[24]
On the other hand, if  does not have
does not have  linearly independent eigenvectors associated with it, then
linearly independent eigenvectors associated with it, then  is not diagonalizable.[25][26]
is not diagonalizable.[25][26]
Definition: A vector 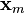 is a generalized eigenvector of rank m of the matrix
is a generalized eigenvector of rank m of the matrix  and corresponding to the eigenvalue
and corresponding to the eigenvalue  if
if
but
Clearly, a generalized eigenvector of rank 1 is an ordinary eigenvector.[28] Every  ×
×  matrix
matrix  has
has  linearly independent generalized eigenvectors associated with it and can be shown to be similar to an "almost diagonal" matrix
linearly independent generalized eigenvectors associated with it and can be shown to be similar to an "almost diagonal" matrix 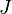 in Jordan normal form.[29] That is, there exists an invertible matrix
in Jordan normal form.[29] That is, there exists an invertible matrix  such that
such that 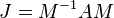 .[30] The matrix
.[30] The matrix  in this case is called a generalized modal matrix for
in this case is called a generalized modal matrix for  .[31] If
.[31] If  is an eigenvalue of algebraic multiplicity
is an eigenvalue of algebraic multiplicity  , then
, then  will have
will have  linearly independent generalized eigenvectors corresponding to
linearly independent generalized eigenvectors corresponding to  .[32] These results, in turn, provide a straightforward method for computing certain matrix functions of
.[32] These results, in turn, provide a straightforward method for computing certain matrix functions of  .[33]
.[33]
The set spanned by all generalized eigenvectors for a given  , forms the generalized eigenspace for
, forms the generalized eigenspace for  .[34]
.[34]
Examples
Here are some examples to illustrate the concept of generalized eigenvectors. Some of the details will be described later.
Example 1
This example is simple but clearly illustrates the point. This type of matrix is used frequently in textbooks.[35][36][37] Suppose
Then there is only one eigenvalue, 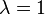 , and its algebraic multiplicity is m = 2.
, and its algebraic multiplicity is m = 2.
There are several ways to see that there will be only one generalized eigenvector. The easiest is to notice that this matrix is in Jordan normal form but is not diagonal. Hence, this matrix is not diagonalizable. Since there is one superdiagonal entry, there will be one generalized eigenvector (or one could note that the vector space  is of dimension 2, so there can be only one generalized eigenvector). Alternatively, one could compute the dimension of the nullspace of
is of dimension 2, so there can be only one generalized eigenvector). Alternatively, one could compute the dimension of the nullspace of 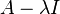 to be p = 1, and thus there are m – p = 1 generalized eigenvectors. (See the nullspace page.)
to be p = 1, and thus there are m – p = 1 generalized eigenvectors. (See the nullspace page.)
Computing the ordinary eigenvector 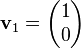 is left to the reader. (See the eigenvector page for examples.) Using this eigenvector, we compute the generalized eigenvector
is left to the reader. (See the eigenvector page for examples.) Using this eigenvector, we compute the generalized eigenvector 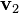 by solving
by solving
Writing out the values:
This simplifies to
The element 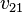 has no restrictions. The generalized eigenvector is then
has no restrictions. The generalized eigenvector is then 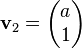 , where a can have any scalar value. The choice of a = 0 is usually the simplest.
, where a can have any scalar value. The choice of a = 0 is usually the simplest.
Note that
so that 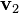 is a generalized eigenvector,
is a generalized eigenvector,
so that 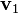 is an ordinary eigenvector, and that
is an ordinary eigenvector, and that 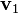 and
and 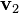 are linearly independent and hence constitute a basis for the vector space
are linearly independent and hence constitute a basis for the vector space  .
.
Example 2
This example is more complex than Example 1. Unfortunately, it is a little difficult to construct an interesting example of low order.[38] The matrix
has eigenvalues 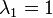 and
and 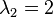 with algebraic multiplicities
with algebraic multiplicities 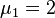 and
and 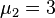 , but geometric multiplicities
, but geometric multiplicities 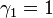 and
and 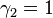 .
.
The generalized eigenspaces of  are calculated below.
are calculated below.
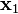 is the ordinary eigenvector associated with
is the ordinary eigenvector associated with  .
.
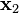 is a generalized eigenvector associated with
is a generalized eigenvector associated with  .
.
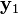 is the ordinary eigenvector associated with
is the ordinary eigenvector associated with  .
.
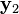 and
and 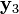 are generalized eigenvectors associated with
are generalized eigenvectors associated with  .
.
This results in a basis for each of the generalized eigenspaces of  .
Together the two chains of generalized eigenvectors span the space of all 5-dimensional column vectors.
.
Together the two chains of generalized eigenvectors span the space of all 5-dimensional column vectors.
An "almost diagonal" matrix 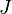 in Jordan normal form, similar to
in Jordan normal form, similar to  is obtained as follows:
is obtained as follows:
where  is a generalized modal matrix for
is a generalized modal matrix for  , the columns of
, the columns of  are a canonical basis for
are a canonical basis for  , and
, and 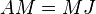 .[39]
.[39]
Jordan chains
Definition: Let 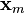 be a generalized eigenvector of rank m corresponding to the matrix
be a generalized eigenvector of rank m corresponding to the matrix  and the eigenvalue
and the eigenvalue  . The chain generated by
. The chain generated by 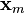 is a set of vectors
is a set of vectors 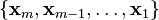 given by
given by
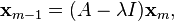
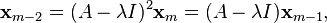
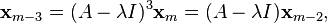
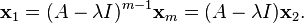
(1)
Thus, in general,
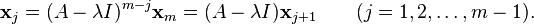
(2)
The vector 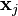 , given by (2), is a generalized eigenvector of rank j corresponding to the eigenvalue
, given by (2), is a generalized eigenvector of rank j corresponding to the eigenvalue  . A chain is a linearly independent set of vectors.[40]
. A chain is a linearly independent set of vectors.[40]
Canonical basis
Definition: A set of n linearly independent generalized eigenvectors is a canonical basis if it is composed entirely of Jordan chains.
Thus, once we have determined that a generalized eigenvector of rank m is in a canonical basis, it follows that the m − 1 vectors 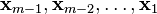 that are in the Jordan chain generated by
that are in the Jordan chain generated by 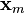 are also in the canonical basis.[41]
are also in the canonical basis.[41]
Let  be an eigenvalue of
be an eigenvalue of  of algebraic multiplicity
of algebraic multiplicity  . First, find the ranks (matrix ranks) of the matrices
. First, find the ranks (matrix ranks) of the matrices 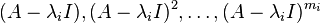 . The integer
. The integer 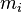 is determined to be the first integer for which
is determined to be the first integer for which 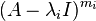 has rank
has rank 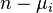 (n being the number of rows or columns of
(n being the number of rows or columns of  , that is,
, that is,  is n × n).
is n × n).
Now define
The variable 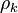 designates the number of linearly independent generalized eigenvectors of rank k corresponding to the eigenvalue
designates the number of linearly independent generalized eigenvectors of rank k corresponding to the eigenvalue  that will appear in a canonical basis for
that will appear in a canonical basis for  . Note that
. Note that
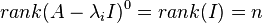 .[42]
.[42]
Computation of generalized eigenvectors
In the preceding sections we have seen techniques for obtaining the n linearly independent generalized eigenvectors of a canonical basis for the vector space  associated with an n × n matrix
associated with an n × n matrix  . These techniques can be combined into a procedure:
. These techniques can be combined into a procedure:
- Solve the characteristic equation of
 for eigenvalues
for eigenvalues  and their algebraic multiplicities
and their algebraic multiplicities  ;
; - For each
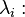
- Determine
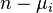 ;
; - Determine
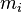 ;
; - Determine
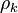 for
for 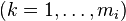 ;
; - Determine each Jordan chain for
 ;
;
- Determine
Example 3
The matrix
has an eigenvalue 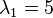 of algebraic multiplicity
of algebraic multiplicity 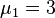 and an eigenvalue
and an eigenvalue 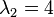 of algebraic multiplicity
of algebraic multiplicity 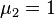 . We also have n = 4. For
. We also have n = 4. For  we have
we have 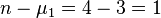 .
.
The first integer 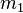 for which
for which 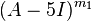 has rank
has rank 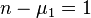 is
is 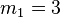 .
.
We now define
Consequently, there will be three linearly independent generalized eigenvectors; one each of ranks 3, 2 and 1. Since  corresponds to a single chain of three linearly independent generalized eigenvectors, we know that there is a generalized eigenvector
corresponds to a single chain of three linearly independent generalized eigenvectors, we know that there is a generalized eigenvector 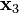 of rank 3 corresponding to
of rank 3 corresponding to  such that
such that
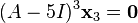
(3)
but
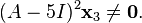
(4)
Equations (3) and (4) represent linear systems that can be solved for 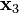 . Let
. Let
Then
and
Thus, in order to satisfy the conditions (3) and (4), we must have 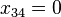 and
and 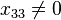 . No restrictions are placed on
. No restrictions are placed on 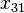 and
and 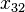 . By choosing
. By choosing 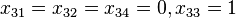 , we obtain
, we obtain
as a generalized eigenvector of rank 3 corresponding to 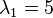 . Note that it is possible to obtain infinitely many other generalized eigenvectors of rank 3 by choosing different values of
. Note that it is possible to obtain infinitely many other generalized eigenvectors of rank 3 by choosing different values of 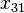 ,
, 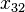 and
and 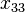 , with
, with 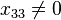 . Our first choice, however, is the simplest.[43]
. Our first choice, however, is the simplest.[43]
Now using equations (1), we obtain 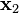 and
and 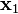 as generalized eigenvectors of rank 2 and 1 respectively, where
as generalized eigenvectors of rank 2 and 1 respectively, where
and
The simple eigenvalue 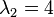 can be dealt with using standard techniques and has an ordinary eigenvector
can be dealt with using standard techniques and has an ordinary eigenvector
A canonical basis for  is
is
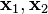 and
and 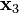 are generalized eigenvectors associated with
are generalized eigenvectors associated with  .
.
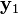 is the ordinary eigenvector associated with
is the ordinary eigenvector associated with  .
.
It should be noted that this is a fairly simple example. In general, the numbers 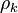 of linearly independent generalized eigenvectors of rank k will not always be equal. That is, there may be several chains of different lengths corresponding to a particular eigenvalue.[44]
of linearly independent generalized eigenvectors of rank k will not always be equal. That is, there may be several chains of different lengths corresponding to a particular eigenvalue.[44]
Generalized modal matrix
Let  be an n × n matrix. A generalized modal matrix
be an n × n matrix. A generalized modal matrix  for
for  is an n × n matrix whose columns, considered as vectors, form a canonical basis for
is an n × n matrix whose columns, considered as vectors, form a canonical basis for  and appear in
and appear in  according to the following rules:
according to the following rules:
- All Jordan chains consisting of one vector (that is, one vector in length) appear in the first columns of
 .
. - All vectors of one chain appear together in adjacent columns of
 .
. - Each chain appears in
 in order of increasing rank (that is, the generalized eigenvector of rank 1 appears before the generalized eigenvector of rank 2 of the same chain, which appears before the generalized eigenvector of rank 3 of the same chain, etc.).[45]
in order of increasing rank (that is, the generalized eigenvector of rank 1 appears before the generalized eigenvector of rank 2 of the same chain, which appears before the generalized eigenvector of rank 3 of the same chain, etc.).[45]
Jordan Normal Form
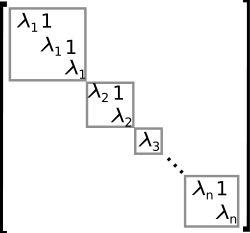
Let  be an n-dimensional vector space; let
be an n-dimensional vector space; let  be a linear map in L(V), the set of all linear maps from
be a linear map in L(V), the set of all linear maps from  into itself; and let
into itself; and let  be the matrix representation of
be the matrix representation of  with respect to some ordered basis. It can be shown that if the characteristic polynomial
with respect to some ordered basis. It can be shown that if the characteristic polynomial 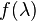 of
of  factors into linear factors, so that
factors into linear factors, so that 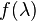 has the form
has the form
where 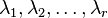 are the distinct eigenvalues of
are the distinct eigenvalues of  , then each
, then each  is the algebraic multiplicity of its corresponding eigenvalue
is the algebraic multiplicity of its corresponding eigenvalue  and
and  is similar to a matrix
is similar to a matrix 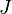 in Jordan normal form, where each
in Jordan normal form, where each  appears
appears  consecutive times on the diagonal, and each entry above each
consecutive times on the diagonal, and each entry above each  (that is, on the superdiagonal) is either 0 or 1; the entry above the first occurrence of each
(that is, on the superdiagonal) is either 0 or 1; the entry above the first occurrence of each  is always 0. All other entries are zero. The matrix
is always 0. All other entries are zero. The matrix 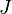 is as close as one can come to a diagonalization of
is as close as one can come to a diagonalization of  . If
. If  is diagonalizable, then all entries above the diagonal are zero.[46] Note that some textbooks have the ones on the subdiagonal, that is, immediately below the main diagonal instead of on the superdiagonal. The eigenvalues are still on the main diagonal.[47][48]
is diagonalizable, then all entries above the diagonal are zero.[46] Note that some textbooks have the ones on the subdiagonal, that is, immediately below the main diagonal instead of on the superdiagonal. The eigenvalues are still on the main diagonal.[47][48]
Every n × n matrix  is similar to a matrix
is similar to a matrix 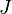 in Jordan normal form, obtained through the similarity transformation
in Jordan normal form, obtained through the similarity transformation 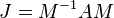 , where
, where  is a generalized modal matrix for
is a generalized modal matrix for  .[49]
.[49]
Example 4
Find a matrix in Jordan normal form that is similar to
Solution: The characteristic equation of  is
is 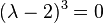 , hence,
, hence, 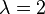 is an eigenvalue of algebraic multiplicity three. Following the procedures of the previous sections, we find that
is an eigenvalue of algebraic multiplicity three. Following the procedures of the previous sections, we find that
and
Thus, 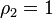 and
and 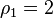 , which implies that a canonical basis for
, which implies that a canonical basis for  will contain one linearly independent generalized eigenvector of rank 2 and two linearly independent generalized eigenvectors of rank 1, or equivalently, one chain of two vectors
will contain one linearly independent generalized eigenvector of rank 2 and two linearly independent generalized eigenvectors of rank 1, or equivalently, one chain of two vectors 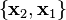 and one chain of one vector
and one chain of one vector 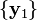 . Designating
. Designating 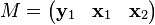 , we find that
, we find that
and
where  is a generalized modal matrix for
is a generalized modal matrix for  , the columns of
, the columns of  are a canonical basis for
are a canonical basis for  , and
, and 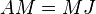 .[50] Note that since generalized eigenvectors themselves are not unique, and since some of the columns of both
.[50] Note that since generalized eigenvectors themselves are not unique, and since some of the columns of both  and
and 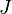 may be interchanged, it follows that both
may be interchanged, it follows that both  and
and 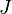 are not unique.[51]
are not unique.[51]
Example 5
In Example 3, we found a canonical basis of linearly independent generalized eigenvectors for a matrix  . A generalized modal matrix for
. A generalized modal matrix for  is
is
A matrix in Jordan normal form, similar to  is
is
so that 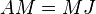 .
.
Applications
Matrix functions
Three of the most fundamental operations which can be performed on square matrices are matrix addition, multiplication by a scalar, and matrix multiplication.[52] These are exactly those operations necessary for defining a polynomial function of an n × n matrix  .[53] If we recall from basic calculus that many functions can be written as a Maclaurin series, then we can define more general functions of matrices quite easily.[54] If
.[53] If we recall from basic calculus that many functions can be written as a Maclaurin series, then we can define more general functions of matrices quite easily.[54] If  is diagonalizable, that is
is diagonalizable, that is
with
then
and the evaluation of the Maclaurin series for functions of  is greatly simplified.[55] For example, to obtain any power k of
is greatly simplified.[55] For example, to obtain any power k of  , we need only compute
, we need only compute 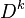 , premultiply
, premultiply 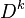 by
by  , and postmultiply the result by
, and postmultiply the result by  .[56]
.[56]
Using generalized eigenvectors, we can obtain the Jordan normal form for  and these results can be generalized to a straightforward method for computing functions of nondiagonalizable matrices.[57] (See Matrix function#Jordan decomposition.)
and these results can be generalized to a straightforward method for computing functions of nondiagonalizable matrices.[57] (See Matrix function#Jordan decomposition.)
Differential equations
Consider the problem of solving the system of linear ordinary differential equations
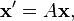
(5)
where
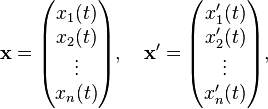 and
and 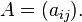
If the matrix  is a diagonal matrix so that
is a diagonal matrix so that 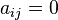 for
for 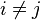 , then the system (5) reduces to a system of n equations which take the form
, then the system (5) reduces to a system of n equations which take the form
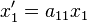
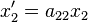
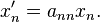
(6)
In this case, the general solution is given by
In the general case, we try to diagonalize  and reduce the system (5) to a system like (6) as follows. If
and reduce the system (5) to a system like (6) as follows. If  is diagonalizable, we have
is diagonalizable, we have 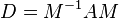 , where
, where  is a modal matrix for
is a modal matrix for  . Substituting
. Substituting 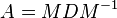 , equation (5) takes the form
, equation (5) takes the form 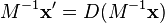 , or
, or
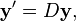
(7)
where
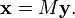
(8)
The solution of (7) is
The solution 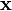 of (5) is then obtained using the relation (8).[58]
of (5) is then obtained using the relation (8).[58]
On the other hand, if  is not diagonalizable, we choose
is not diagonalizable, we choose  to be a generalized modal matrix for
to be a generalized modal matrix for  , such that
, such that 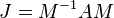 is the Jordan normal form of
is the Jordan normal form of  . The system
. The system 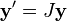 has the form
has the form
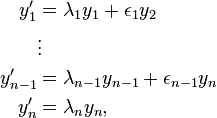
(9)
where the  are the eigenvalues from the main diagonal of
are the eigenvalues from the main diagonal of 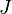 and the
and the  are the ones and zeros from the superdiagonal of
are the ones and zeros from the superdiagonal of 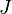 . The system (9) is often more easily solved than (5). We may solve the last equation in (9) for
. The system (9) is often more easily solved than (5). We may solve the last equation in (9) for  , obtaining
, obtaining 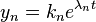 . We then substitute this solution for
. We then substitute this solution for  into the next to last equation in (9) and solve for
into the next to last equation in (9) and solve for 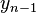 . Continuing this procedure, we work through (9) from the last equation to the first, solving the entire system for
. Continuing this procedure, we work through (9) from the last equation to the first, solving the entire system for  . The solution
. The solution 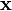 is then obtained using the relation (8).[59]
is then obtained using the relation (8).[59]
Notes
- ↑ Bronson (1970, p. 189)
- ↑ Beauregard & Fraleigh (1973, p. 310)
- ↑ Nering (1970, p. 118)
- ↑ Golub & Van Loan (1996, p. 316)
- ↑ Beauregard & Fraleigh (1973, p. 319)
- ↑ Bronson (1970, pp. 194-195)
- ↑ Golub & Van Loan (1996, p. 311)
- ↑ Bronson (1970, p. 196)
- ↑ Bronson (1970, p. 189)
- ↑ Beauregard & Fraleigh (1973, p. 316-318)
- ↑ Nering (1970, p. 118)
- ↑ Anton (1987, pp. 301-302)
- ↑ Beauregard & Fraleigh (1973, p. 266)
- ↑ Burden & Faires (1993, p. 401)
- ↑ Golub & Van Loan (1996, pp. 310-311)
- ↑ Harper (1976, p. 58)
- ↑ Herstein (1964, p. 225)
- ↑ Kreyszig (1972, pp. 273,684)
- ↑ Nering (1970, p. 104)
- ↑ Burden & Faires (1993, p. 401)
- ↑ Beauregard & Fraleigh (1973, pp. 270-274)
- ↑ Bronson (1970, pp. 179-183)
- ↑ Bronson (1970, p. 181)
- ↑ Bronson (1970, p. 179)
- ↑ Beauregard & Fraleigh (1973, pp. 270-274)
- ↑ Bronson (1970, pp. 179-183)
- ↑ Bronson (1970, p. 189)
- ↑ Bronson (1970, pp. 190,202)
- ↑ Bronson (1970, pp. 189,203)
- ↑ Bronson (1970, pp. 206-207)
- ↑ Bronson (1970, p. 205)
- ↑ Bronson (1970, p. 196)
- ↑ Bronson (1970, pp. 189,209-215)
- ↑ Nering (1970, p. 118)
- ↑ Nering (1970, p. 118)
- ↑ Herstein (1964, p. 261)
- ↑ Beauregard & Fraleigh (1973, p. 310)
- ↑ Nering (1970, pp. 122,123)
- ↑ Bronson (1970, pp. 189-209)
- ↑ Bronson (1970, pp. 194-195)
- ↑ Bronson (1970, pp. 196,197)
- ↑ Bronson (1970, pp. 197,198)
- ↑ Bronson (1970, pp. 190-191)
- ↑ Bronson (1970, pp. 197-198)
- ↑ Bronson (1970, p. 205)
- ↑ Beauregard & Fraleigh (1973, p. 311)
- ↑ Cullen (1966, p. 114)
- ↑ Franklin (1968, p. 122)
- ↑ Bronson (1970, p. 207)
- ↑ Bronson (1970, pp. 208)
- ↑ Bronson (1970, p. 206)
- ↑ Beauregard & Fraleigh (1973, pp. 57-61)
- ↑ Bronson (1970, p. 104)
- ↑ Bronson (1970, p. 105)
- ↑ Bronson (1970, p. 184)
- ↑ Bronson (1970, p. 185)
- ↑ Bronson (1970, pp. 209-218)
- ↑ Beauregard & Fraleigh (1973, pp. 274-275)
- ↑ Beauregard & Fraleigh (1973, p. 317)
References
- Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
- Axler, Sheldon (1997). Linear Algebra Done Right (2nd ed.). Springer. ISBN 978-0-387-98258-8.
- Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Co., ISBN 0-395-14017-X
- Bronson, Richard (1970), Matrix Methods: An Introduction, New York: Academic Press, LCCN 70097490
- Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5th ed.), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3
- Cullen, Charles G. (1966), Matrices and Linear Transformations, Reading: Addison-Wesley, LCCN 66021267
- Franklin, Joel N. (1968), Matrix Theory, Englewood Cliffs: Prentice-Hall, LCCN 68016345
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Baltimore: Johns Hopkins University Press, ISBN 0-8018-5414-8
- Harper, Charlie (1976), Introduction to Mathematical Physics, New Jersey: Prentice-Hall, ISBN 0-13-487538-9
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 0-471-50728-8
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
| ||||||||||||||||||