Job plot

A Job plot (also known as the method of continuous variation or Job's method; named after P. Job) is used to determine the stoichiometry of a binding event. This method is widely used in analytical chemistry, instrumental analysis, and advanced chemical equilibrium texts and research articles.

In 1928, Paul Job published a paper entitled Formation and Stability of Inorganic Complexes in Solution. He looked into the study of ion associations. Part of his research focused on relating UV absorption to the mole fraction of Tl(NO3) in a Tl(NO3)/NH3 solution. [1] Plotting the absorbance versus mole fraction yielded the first Job Plot, which provided Job with information about equilibrium complexes and thus complexes present in solution.

In solutions where two species are present (i.e. species A and species B), one species (A) may bind to the other species (B). In some cases, more than one A will bind with a single B. One way to determine the amount of A binding to B is by using a Job plot.

In this method, the total molar concentration of the two binding partners (e.g. a protein and ligand or a metal and a ligand) are held constant, but their mole fractions are varied. An observable that is proportional to complex formation (such as absorption signal or enzymatic activity) is plotted against the mole fractions of these two components.

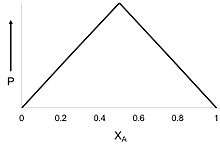
A simple Job Plot showing how a physical property changes upon changing the mole fraction of compound A.


χA is the mole fraction of compound A and P is the physical property being measured to understand complex formation. This property is most often times UV absorbance. [2]

The maximum (or minimum) on the plot corresponds to the stoichiometry of the two species[3] if sufficiently high concentrations are used. The plot also provides insight to understand the equilibrium constant (Keq) of complex formation. A greater curvature leads to a more evenly distributed equilibrium, while a more triangle-shaped plot signifies a large Keq. [4] Further, after determining the equilibrium constant, we can determine what complexes (ratio of A and B) are present in solution. [5] In addition, the peak of the Job Plot corresponds to the mole fraction of ligands bound to a molecule, which can is important for studying ligand field theory. [6] An early work of I. Ostromisslensky describes essentially this approach [7]

There are several conditions that must be met in order for Job's method to be applicable:[8]

  1. The system must conform to Beer's law
  2. One complex must predominate under the conditions of the experiment
  3. The Total concentration of the two binding partners must be maintained constant
  4. pH and ionic strength must be maintained constant

References

  1. ↑ Job, P. Annali di Chimica Applicata (1928) 9, 113-203
  2. ↑ Renny, J. S.; Tomasevich, L. L.; Tallmadge, E. H.; Collum, D. B. Method of Continuous Variations: applications of job plots to the molecular associations in organometallic chemistry. Angew Chem Int Ed Engl (2013) 46, 11998 – 2013.
  3. ↑ Huang, C.Y. Determination of Binding Stoichiometry by the Continuous Variation Method: The Job Plot. Methods in Enzymology (1982) 87, 509-525.
  4. ↑
  5. ↑ Facchiano, A. and Ragone, R. Modification of Job’s method for determining the stoichiometry of protein – protein complexes. Analytical Biochemistry (2003) 313, 170 – 172.
  6. ↑ Hauser, A. Ligand Field Theoretical Considerations. Adv Polym Sci (2004) 233, 49 – 58.
  7. ↑ Ostromisslensky, I., Berichte der Deutschen Chemischen Gesellschaft (1911), 44 (1), 268-273.
  8. ↑ MacCarthy, Patrick; Zachary D. Hill (February 1986). "Novel Approach to Job's Method". Journal of Chemical Education 63 (2): 162–167. doi:10.1021/ed063p162.
This article is issued from Wikipedia - version of the Thursday, December 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.