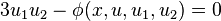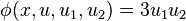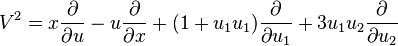Jet bundle
In differential geometry, the jet bundle is a certain construction that makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form. Jets may also be seen as the coordinate free versions of Taylor expansions.
Historically, jet bundles are attributed to Ehresmann, and were an advance on the method (prolongation) of Élie Cartan, of dealing geometrically with higher derivatives, by imposing differential form conditions on newly introduced formal variables. Jet bundles are sometimes called sprays, although sprays usually refer more specifically to the associated vector field induced on the corresponding bundle (e.g., the geodesic spray on Finsler manifolds.)
More recently, jet bundles have appeared as a concise way to describe phenomena associated with the derivatives of maps, particularly those associated with the calculus of variations. Consequently, the jet bundle is now recognized as the correct domain for a geometrical covariant field theory and much work is done in general relativistic formulations of fields using this approach.
Jets
Suppose M is an m-dimensional manifold and that (E, π, M) is a fiber bundle. For p ∈ M, let Γ(π) denote the set of all local sections whose domain contains p. Let I = (I(1), I(2), ..., I(m)) be a multi-index (an ordered m-tuple of integers), then
Define the local sections σ, η ∈ Γ(π) to have the same r-jet at p if
The relation that two maps have the same r-jet is an equivalence relation. An r-jet is an equivalence class under this relation, and the r-jet with representative σ is denoted 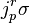 . The integer r is also called the order of the jet, p is its source and σ(p) is its target.
. The integer r is also called the order of the jet, p is its source and σ(p) is its target.
Jet manifolds
The r-th jet manifold of π is the set
and is denoted Jr(π). We may define projections πr and πr,0 called the source and target projections respectively, by
If 1 ≤ k ≤ r, then the k-jet projection is the function πr,k defined by
From this definition, it is clear that πr = π o πr,0 and that if 0 ≤ m ≤ k, then πr,m = πk,m o πr,k. It is conventional to regard πr,r = idJr(π), the identity map on Jr(π) and to identify J0(π) with E.
The functions πr,k, πr,0 and πr are smooth surjective submersions.

A coordinate system on E will generate a coordinate system on Jr(π). Let (U, u) be an adapted coordinate chart on E, where u = (xi, uα). The induced coordinate chart (Ur, ur) on Jr(π) is defined by
where
and the 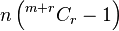 functions
functions
are specified by
and are known as the derivative coordinates.
Given an atlas of adapted charts (U, u) on E, the corresponding collection of charts (Ur, ur) is a finite-dimensional C∞ atlas on Jr(π).
Jet bundles
Since the atlas on each Jr(π) defines a manifold, the triples (Jr(π), πr,k, Jk(π)), (Jr(π), πr,0, E) and (Jr(π), πr, M) all define fibered manifolds. In particular, if (E, π, M) is a fiber bundle, the triple (Jr(π), πr, M) defines the r-th jet bundle of π.
If W ⊂ M is an open submanifold, then
If p ∈ M, then the fiber 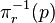 is denoted
is denoted 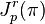 .
.
Let σ be a local section of π with domain W ⊂ M. The r-th jet prolongation of σ is the map jrσ: W → Jr(π) defined by
Note that πr o jrσ = idW, so jrσ really is a section. In local coordinates, jrσ is given by
We identify j0σ with σ.
Example
If π is the trivial bundle (M × R, pr1, M), then there is a canonical diffeomorphism between the first jet bundle J1(π) and T*M × R. To construct this diffeomorphism, for each σ in ΓM(π) write 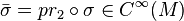 .
.
Then, whenever p ∈ M
Consequently, the mapping
is well-defined and is clearly injective. Writing it out in coordinates shows that it is a diffeomorphism, because if (xi, u) are coordinates on M × R, where u = idR is the identity coordinate, then the derivative coordinates ui on J1(π) correspond to the coordinates ∂i on T*M.
Likewise, if π is the trivial bundle (R × M, pr1, R), then there exists a canonical diffeomorphism between J1(π) and R × TM.
Contact structure
The space Jr(π) carries a natural distribution, that is, a sub-bundle of the tangent bundle TJr(π)), called the Cartan distribution. The Cartan distribution is spanned by all tangent planes to graphs of holonomic sections; that is, sections of the form jrφ for φ a section of π.
The annihilator of the Cartan distribution is a space of differential one-forms called contact forms, on Jr(π). The space of differential one-forms on Jr(π) is denoted by 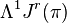 and the space of contact forms is denoted by
and the space of contact forms is denoted by 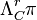 . A one form is a contact form provided its pullback along every prolongation is zero. In other words,
. A one form is a contact form provided its pullback along every prolongation is zero. In other words, 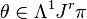 is a contact form if and only if
is a contact form if and only if
for all local sections σ of π over M.
The Cartan distribution is the main geometrical structure on jet spaces and plays an important role in the geometric theory of partial differential equations. The Cartan distributions are completely non-integrable. In particular, they are not involutive. The dimension of the Cartan distribution grows with the order of the jet space. However, on the space of infinite jets J∞ the Cartan distribution becomes involutive and finite-dimensional: its dimension coincides with the dimension of the base manifold M.
Example
Let us consider the case (E, π, M), where E ≃ R2 and M ≃ R. Then, (J1(π), π, M) defines the first jet bundle, and may be coordinated by (x, u, u1), where
for all p ∈ M and σ in Γp(π). A general 1-form on J1(π) takes the form
A section σ in Γp(π) has first prolongation
Hence, (j1σ)*θ can be calculated as
This will vanish for all sections σ if and only if c = 0 and a = −bσ′(x). Hence, θ = b(x, u, u1)θ0 must necessarily be a multiple of the basic contact form θ0 = du − u1dx. Proceeding to the second jet space J2(π) with additional coordinate u2, such that
a general 1-form has the construction
This is a contact form if and only if
which implies that e = 0 and a = −bσ′(x) − cσ′′(x). Therefore, θ is a contact form if and only if
where θ1 = du1 − u2dx is the next basic contact form (Note that here we are identifying the form θ0 with its pull-back 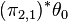 to J2(π)).
to J2(π)).
In general, providing x, u ∈ R, a contact form on Jr+1(π) can be written as a linear combination of the basic contact forms
where 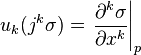 .
.
Similar arguments lead to a complete characterization of all contact forms.
In local coordinates, every contact one-form on Jr+1(π) can be written as a linear combination
with smooth coefficients 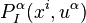 of the basic contact forms
of the basic contact forms
|I| is known as the order of the contact form 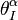 . Note that contact forms on Jr+1(π) have orders at most r. Contact forms provide a characterization of those local sections of πr+1 which are prolongations of sections of π.
. Note that contact forms on Jr+1(π) have orders at most r. Contact forms provide a characterization of those local sections of πr+1 which are prolongations of sections of π.
Let ψ ∈ ΓW(πr+1), then ψ = jr+1σ where σ ∈ ΓW(π) if and only if 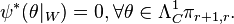
Vector fields
A general vector field on the total space E, coordinated by 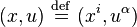 , is
, is
A vector field is called horizontal, meaning that all the vertical coefficients vanish, if φα = 0.
A vector field is called vertical, meaning that all the horizontal coefficients vanish, if ρi = 0.
For fixed (x, u), we identify
having coordinates (x, u, ρi, φα), with an element in the fiber TxuE of TE over (x,u) in E, called a tangent vector in TE. A section
is called a vector field on E' with
and ψ in Γ(TE).
The jet bundle Jr(π) is coordinated by 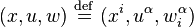 . For fixed (x,u,w), identify
. For fixed (x,u,w), identify
having coordinates 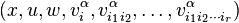 , with an element in the fiber
, with an element in the fiber 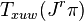 of TJr(π) over (x, u, w) ∈ Jr(π), called a tangent vector in TJr(π). Here,
of TJr(π) over (x, u, w) ∈ Jr(π), called a tangent vector in TJr(π). Here,
are real-valued functions on Jr(π). A section
is a vector field on Jr(π), and we say 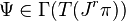 .
.
Partial differential equations
Let (E, π, M) be a fiber bundle. An r-th order partial differential equation on π is a closed embedded submanifold S of the jet manifold Jr(π). A solution is a local section σ ∈ ΓW(π) satisfying 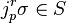 , for all p in M.
, for all p in M.
Let us consider an example of a first order partial differential equation.
Example
Let π be the trivial bundle (R2 × R, pr1, R2) with global coordinates (x1, x2, u1). Then the map F : J1(π) → R defined by
gives rise to the differential equation
which can be written
The particular section σ: R2 → R2 × R defined by
has first prolongation given by
and is a solution of this differential equation, because
and so 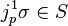 for every p ∈ R2.
for every p ∈ R2.
Jet Prolongation
A local diffeomorphism ψ: Jr(π) → Jr(π) defines a contact transformation of order r if it preserves the contact ideal, meaning that if θ is any contact form on Jr(π), then ψ*θ is also a contact form.
The flow generated by a vector field Vr on the jet space Jr(π) forms a one-parameter group of contact transformations if and only if the Lie derivative 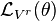 of any contact form θ preserves the contact ideal.
of any contact form θ preserves the contact ideal.
Let us begin with the first order case. Consider a general vector field V1 on J1(π), given by
We now apply 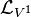 to the basic contact forms
to the basic contact forms 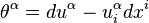 , and obtain
, and obtain
where we have expanded the exterior derivative of the functions in terms of their coordinates. Next, we note that
and so we may write
Therefore, V1 determines a contact transformation if and only if the coefficients of dxi and 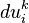 in the formula vanish. The latter requirements imply the contact conditions
in the formula vanish. The latter requirements imply the contact conditions
The former requirements provide explicit formulae for the coefficients of the first derivative terms in V1:
where
denotes the zeroth order truncation of the total derivative Di.
Thus, the contact conditions uniquely prescribe the prolongation of any point or contact vector field. That is, if 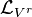 satisfies these equations, Vr is called the r-th prolongation of V to a vector field on Jr(π).
satisfies these equations, Vr is called the r-th prolongation of V to a vector field on Jr(π).
These results are best understood when applied to a particular example. Hence, let us examine the following.
Example
Let us consider the case (E, π, M), where E ≅ R2 and M ≃ R. Then, (J1(π), π, E) defines the first jet bundle, and may be coordinated by (x, u, u1), where
for all p ∈ M and σ in Γp(π). A contact form on J1(π) has the form
Let us consider a vector V on E, having the form
Then, the first prolongation of this vector field to J1(π) is
If we now take the Lie derivative of the contact form with respect to this prolonged vector field, 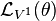 , we obtain
, we obtain
But, we may identify du = θ + u1dx. Thus, we get
Hence, for 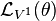 to preserve the contact ideal, we require
to preserve the contact ideal, we require
And so the first prolongation of V to a vector field on J1(π) is
Let us also calculate the second prolongation of V to a vector field on J2(π). We have 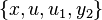 as coordinates on J2(π). Hence, the prolonged vector has the form
as coordinates on J2(π). Hence, the prolonged vector has the form
The contacts forms are
To preserve the contact ideal, we require
Now, θ has no u2 dependency. Hence, from this equation we will pick up the formula for ρ, which will necessarily be the same result as we found for V1. Therefore, the problem is analogous to prolonging the vector field V1 to J2(π). That is to say, we may generate the r-th prolongation of a vector field by recursively applying the Lie derivative of the contact forms with respect to the prolonged vector fields, r times. So, we have
and so
Therefore, the Lie derivative of the second contact form with respect to V2 is
Again, let us identify du = θ + u1dx and du1 = θ1 + u2dx. Then we have
Hence, for 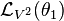 to preserve the contact ideal, we require
to preserve the contact ideal, we require
And so the second prolongation of V to a vector field on J2(π) is
Note that the first prolongation of V can be recovered by omitting the second derivative terms in V2, or by projecting back to J1(π).
Infinite Jet Spaces
The inverse limit of the sequence of projections 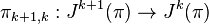 gives rise to the infinite jet space J∞(π). A point
gives rise to the infinite jet space J∞(π). A point 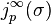 is the equivalence class of sections of π that have the same k-jet in p as σ for all values of k. The natural projection π∞ maps
is the equivalence class of sections of π that have the same k-jet in p as σ for all values of k. The natural projection π∞ maps 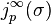 into p.
into p.
Just by thinking in terms of coordinates, J∞(π) appears to be an infinite-dimensional geometric object. In fact, the simplest way of introducing a differentiable structure on J∞(π), not relying on differentiable charts, is given by the differential calculus over commutative algebras. Dual to the sequence of projections 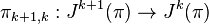 of manifolds is the sequence of injections
of manifolds is the sequence of injections 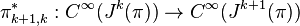 of commutative algebras. Let's denote
of commutative algebras. Let's denote 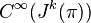 simply by
simply by 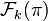 . Take now the direct limit
. Take now the direct limit 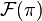 of the
of the 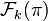 's. It will be a commutative algebra, which can be assumed to be the smooth functions algebra over the geometric object J∞(π). Observe that
's. It will be a commutative algebra, which can be assumed to be the smooth functions algebra over the geometric object J∞(π). Observe that 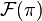 , being born as a direct limit, carries an additional structure: it is a filtered commutative algebra.
, being born as a direct limit, carries an additional structure: it is a filtered commutative algebra.
Roughly speaking, a concrete element 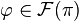 will always belong to some
will always belong to some 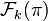 , so it is a smooth function on the finite-dimensional manifold Jk(π) in the usual sense.
, so it is a smooth function on the finite-dimensional manifold Jk(π) in the usual sense.
Infinitely prolonged PDEs
Given a k-th order system of PDEs E ⊆ Jk(π), the collection I(E) of vanishing on E smooth functions on J∞(π) is an ideal in the algebra 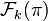 , and hence in the direct limit
, and hence in the direct limit 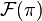 too.
too.
Enhance I(E) by adding all the possible compositions of total derivatives applied to all its elements. This way we get a new ideal I of 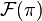 which is now closed under the operation of taking total derivative. The submanifold E(∞) of J∞(π) cut out by I is called the infinite prolongation of E.
which is now closed under the operation of taking total derivative. The submanifold E(∞) of J∞(π) cut out by I is called the infinite prolongation of E.
Geometrically, E(∞) is the manifold of formal solutions of E. A point 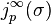 of E(∞) can be easily seen to be represented by a section σ whose k-jet's graph is tangent to E at the point
of E(∞) can be easily seen to be represented by a section σ whose k-jet's graph is tangent to E at the point 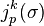 with arbitrarily high order of tangency.
with arbitrarily high order of tangency.
Analytically, if E is given by φ = 0, a formal solution can be understood as the set of Taylor coefficients of a section σ in a point p that make vanish the Taylor series of 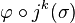 at the point p.
at the point p.
Most importantly, the closure properties of I imply that E(∞) is tangent to the infinite-order contact structure  on J∞(π), so that by restricting
on J∞(π), so that by restricting  to E(∞) one gets the diffiety
to E(∞) one gets the diffiety 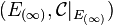 , and can study the associated C-spectral sequence.
, and can study the associated C-spectral sequence.
Remark
This article has defined jets of local sections of a bundle, but it is possible to define jets of functions f: M → N, where M and N are manifolds; the jet of f then just corresponds to the jet of the section
- grf: M → M × N
- grf(p) = (p, f(p))
(grf is known as the graph of the function f) of the trivial bundle (M × N, π1, M). However, this restriction does not simplify the theory, as the global triviality of π does not imply the global triviality of π1.
See also
References
- Ehresmann, C., "Introduction à la théorie des structures infinitésimales et des pseudo-groupes de Lie." Geometrie Differentielle, Colloq. Inter. du Centre Nat. de la Recherche Scientifique, Strasbourg, 1953, 97-127.
- Kolář, I., Michor, P., Slovák, J., Natural operations in differential geometry. Springer-Verlag: Berlin Heidelberg, 1993. ISBN 3-540-56235-4, ISBN 0-387-56235-4.
- Saunders, D. J., "The Geometry of Jet Bundles", Cambridge University Press, 1989, ISBN 0-521-36948-7
- Krasil'shchik, I. S., Vinogradov, A. M., [et al.], "Symmetries and conservation laws for differential equations of mathematical physics", Amer. Math. Soc., Providence, RI, 1999, ISBN 0-8218-0958-X.
- Olver, P. J., "Equivalence, Invariants and Symmetry", Cambridge University Press, 1995, ISBN 0-521-47811-1
- Giachetta, G., Mangiarotti, L., Sardanashvily, G., "Advanced Classical Field Theory", World Scientific, 2009, ISBN 978-981-283-895-7
- Sardanashvily, G., Advanced Differential Geometry for Theoreticians. Fiber bundles, jet manifolds and Lagrangian theory", Lambert Academic Publishing, 2013, ISBN 978-3-659-37815-7; arXiv: 0908.1886
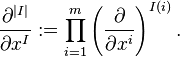
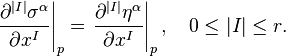
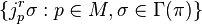
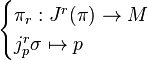
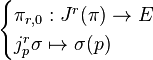
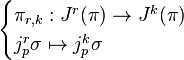
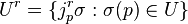
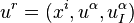
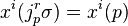
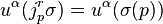
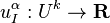
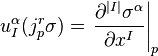
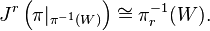
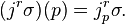
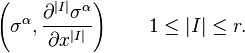
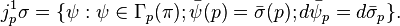
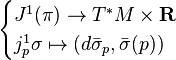
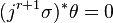
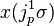
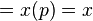
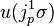
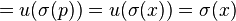
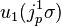
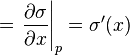
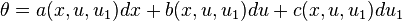
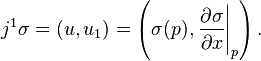
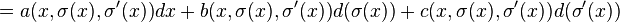
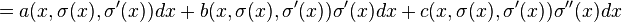
![= [\, a(x, \sigma(x), \sigma'(x)) + b(x, \sigma(x), \sigma'(x))\sigma'(x) + c(x, \sigma(x),\sigma'(x))\sigma''(x)\, ]dx \,](../I/m/1a2fcd49dea1e4eedbed491f67455d6e.png)
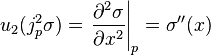
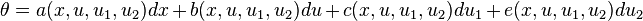
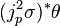
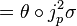
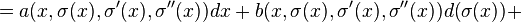
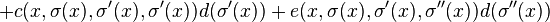
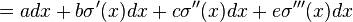
![= [\, a + b\sigma'(x) + c\sigma''(x) + e\sigma'''(x)\,]dx\,](../I/m/f6eab79c6aac103b69f730d1dc9cd3d9.png)
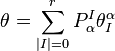
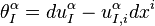
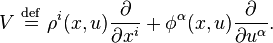
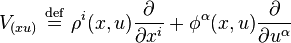
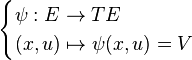
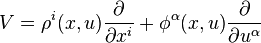
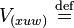
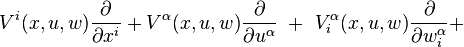
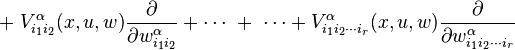
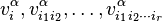
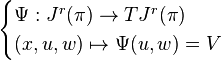
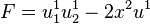
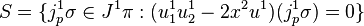
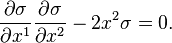
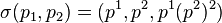
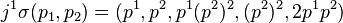
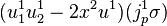
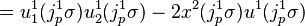
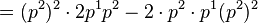
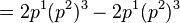
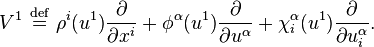
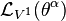
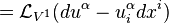
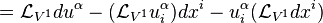
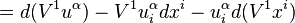
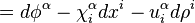
![= \frac{\partial \phi^{\alpha}}{\partial x^{i}}\, dx^{i} + \frac{\partial \phi^{\alpha}}{\partial u^{k}}\, du^{k} + \frac{\partial \phi^{\alpha}}{\partial u^{k}_{i}}\, du^{k}_{i} - \chi^{\alpha}_{i}dx^{i} - u_{i}^{\alpha}\left[ \frac{\partial \rho^{i}}{\partial x^{m}}\, dx^{m} + \frac{\partial \rho^{i}}{\partial u^{k}}\, du^{k} + \frac{\partial \rho^{i}}{\partial u^{k}_{m}}\, du^{k}_{m} \right ] \,](../I/m/1d901e9bdc6be462c2ccaadc36a36da1.png)

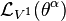
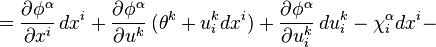
![-u_{l}^{\alpha} \left[ \frac{\partial \rho^{l}}{\partial x^{i}}\, dx^{i} + \frac{\partial \rho^{l}}{\partial u^{k}}\, (\theta^{k} + u_{i}^{k}dx^{i}) + \frac{\partial \rho^{l}}{\partial u^{k}_{i}}\, du^{k}_{i} \right ] \,](../I/m/6948d953e5d486706866aefe1879d382.png)
![= \left[ \frac{\partial \phi^{\alpha}}{\partial x^{i}} + \frac{\partial \phi^{\alpha}}{\partial u^{k}}u_{i}^{k} - u_{l}^{\alpha}\left(\frac{\partial \rho^{l}}{\partial x^{i}} + \frac{\partial \rho^{l}}{\partial u^{k}}u_{i}^{k}\right)- \chi^{\alpha}_{i}\right]\, dx^{i} + \left[ \frac{\partial \phi^{\alpha}}{\partial u^{k}_{i}} - u_{l}^{\alpha}\frac{\partial \rho^{l}}{\partial u^{k}_{i}}\right]\, du^{k}_{i} + \,](../I/m/75317a997f1a9f3c9eaf2413f88c7ae5.png)
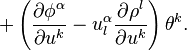
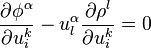
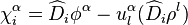
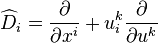
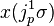
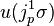
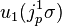
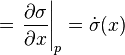
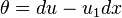
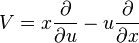
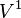
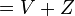
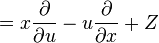
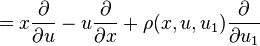
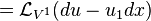
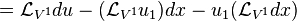
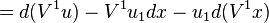
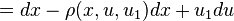
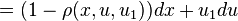
![= [\,1 - \rho(x,u,u_{1})\,]dx + u_{1}(\theta + u_{1}dx) \,](../I/m/487795edfcde6a1d65096f2a5dfe6b63.png)
![= [\,1 + u_{1}u_{1} - \rho(x,u,u_{1})\,]dx + u_{1}\theta \,](../I/m/3a4c0da7ac895bc45e0b98a6b3fbeb0e.png)
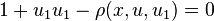
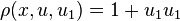
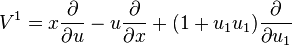
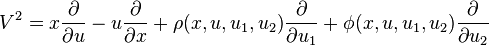

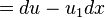
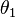

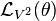
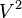
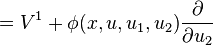
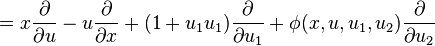
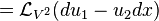
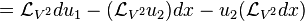
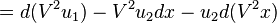
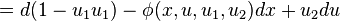
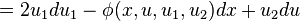
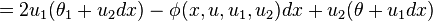
![= [\, 3u_{1}u_{2} - \phi(x,u,u_{1},u_{2})\,]dx + u_{2}\theta + 2u_{1}\theta_{1} \,](../I/m/4070b1544e2f21b2a6397e35fce5dc5a.png)