Janko group J3

Algebraic structure → Group theory Group theory
Basic notions Subgroup Normal subgroup Quotient group (Semi-)direct product Group homomorphisms kernel image direct sum wreath product simple finite infinite continuous multiplicative additive cyclic abelian dihedral nilpotent solvable List of group theory topics Glossary of group theory
Finite groups Classification of finite simple groups cyclic alternating Lie type sporadic Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Symmetric group Sn Klein four-group V Dihedral group Dn Quaternion group Q Dicyclic group Dicn
Discrete groups Lattices Integers (Z) Lattice Modular groups PSL(2,Z) SL(2,Z)
Topological / Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Elliptic curve Linear algebraic group Abelian variety

In the area of modern algebra known as group theory, the Janko group J₃ or the Higman-Janko-McKay group HJM is a sporadic simple group of order

   2⁷ · 3⁵ · 5 · 17 · 19 = 50232960

≈ 5×10⁷.

History and properties

J₃ is one of the 26 Sporadic groups and was predicted by Zvonimir Janko in 1969 as one of two new simple groups having 2¹⁺⁴:A₅ as a centralizer of an involution (the other is the Janko group J₂). J₃ was shown to exist by Graham Higman and John McKay (1969).

J₃ is one of the 6 sporadic simple groups called the pariahs because (Griess 1982) showed that it is not a subquotient of the monster group.

J₃ has an outer automorphism group of order 2 and a Schur multiplier of order 3, and its triple cover has a unitary 9-dimensional representation over the finite field with 4 elements. Weiss (1982) constructed it via an underlying geometry. It has a modular representation of dimension eighteen over the finite field with 9 elements. It has a complex projective representation of dimension eighteen.

Presentations

In terms of generators a, b, c, and d its automorphism group J₃:2 can be presented as

A presentation for J₃ in terms of (different) generators a, b, c, d is

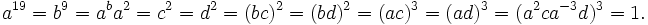
Maximal subgroups

Finkelstein & Rudvalis (1974) found the 9 conjugacy classes of maximal subgroups of J₃ as follows:

• PSL(2,16):2, order 8160
• PSL(2,19), order 3420
• PSL(2,19), conjugate to preceding class in J₃:2
• 2⁴: (3 × A₅), order 2880
• PSL(2,17), order 2448
• (3 × A₆):2₂, order 2160 - normalizer of subgroup of order 3
• 3²⁺¹⁺²:8, order 1944 - normalizer of Sylow 3-subgroup
• 2¹⁺⁴:A₅, order 1920 - centralizer of involution
• 2²⁺⁴: (3 × S₃), order 1152

References

• Finkelstein, L.; Rudvalis, A. (1974), "The maximal subgroups of Janko's simple group of order 50,232,960", Journal of Algebra 30: 122–143, doi:10.1016/0021-8693(74)90196-3, ISSN 0021-8693, MR 0354846 
• R. L. Griess, Jr., The Friendly Giant, Inventiones Mathematicae 69 (1982), 1-102. p. 93: proof that J₃ is a pariah.
• Higman, Graham; McKay, John (1969), "On Janko's simple group of order 50,232,960", Bull. London Math. Soc. 1: 89–94; correction p. 219, doi:10.1112/blms/1.1.89, MR 0246955 
• Z. Janko, Some new finite simple groups of finite order, 1969 Symposia Mathematica (INDAM, Rome, 1967/68), Vol. 1 pp. 25-64 Academic Press, London, and in The theory of finite groups (Edited by Brauer and Sah) p. 63-64, Benjamin, 1969.MR 0244371
• Richard Weiss, "A Geometric Construction of Janko's Group J₃", Math. Zeitschrift 179 pp 91-95 (1982)

External links

• MathWorld: Janko Groups
• Atlas of Finite Group Representations: J₃ version 2
• Atlas of Finite Group Representations: J₃ version 3