James Clerk Maxwell

James Clerk Maxwell

James Clerk Maxwell (1831–1879)
Born (1831-06-13)13 June 1831
Edinburgh, Scotland
Died 5 November 1879(1879-11-05) (aged 48)
Cambridge, England
Citizenship British
Nationality Scottish
Fields Physics and Mathematics
Institutions Marischal College, Aberdeen
King's College, London
University of Cambridge
Alma mater University of Edinburgh
University of Cambridge
Academic advisors William Hopkins
Notable students George Chrystal
John Henry Poynting
Known for Maxwell's equations
Maxwell distribution
Maxwell's demon
Maxwell's discs
Maxwell speed distribution
Maxwell's theorem
Maxwell material
Generalized Maxwell model
Displacement current
Maxwell coil
Maxwell's wheel[1]
Notable awards Smith's Prize (1854)
Adams Prize (1857)
Rumford Medal (1860)
Keith Prize (1869–71)

Signature

James Clerk Maxwell's birthplace at 14 India Street, Edinburgh

James Clerk Maxwell FRS FRSE (13 June 1831 – 5 November 1879) was a Scottish[2][3] scientist in the field of mathematical physics.[4] His most notable achievement was to formulate the classical theory of electromagnetic radiation, bringing together for the first time electricity, magnetism, and light as manifestations of the same phenomenon. Maxwell's equations for electromagnetism have been called the "second great unification in physics"[5] after the first one realised by Isaac Newton.

With the publication of A Dynamical Theory of the Electromagnetic Field in 1865, Maxwell demonstrated that electric and magnetic fields travel through space as waves moving at the speed of light. Maxwell proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena.[6] The unification of light and electrical phenomena led to the prediction of the existence of radio waves.

Maxwell helped develop the Maxwell–Boltzmann distribution, a statistical means of describing aspects of the kinetic theory of gases. He is also known for presenting the first durable colour photograph in 1861 and for his foundational work on analysing the rigidity of rod-and-joint frameworks (trusses) like those in many bridges.

His discoveries helped usher in the era of modern physics, laying the foundation for such fields as special relativity and quantum mechanics. Many physicists regard Maxwell as the 19th-century scientist having the greatest influence on 20th-century physics. His contributions to the science are considered by many to be of the same magnitude as those of Isaac Newton and Albert Einstein.[7] In the millennium poll—a survey of the 100 most prominent physicists—Maxwell was voted the third greatest physicist of all time, behind only Newton and Einstein.[8] On the centenary of Maxwell's birthday, Einstein described Maxwell's work as the "most profound and the most fruitful that physics has experienced since the time of Newton".[9]

Life

Early life, 1831–39

James Clerk Maxwell was born on 13 June 1831 at 14 India Street, Edinburgh, to John Clerk, an advocate, and Frances Cay.[10][11] His father was a man of comfortable means[12] of the Clerk family of Penicuik, holders of the baronetcy of Clerk of Penicuik. His father's brother was the 6th Baronet.[13] He had been born "John Clerk", adding the surname Maxwell to his own after he inherited the Middlebie country estate near Corsock, Kirkcudbrightshire, from connections to the Maxwell family, themselves members of the peerage.[10] James was the first cousin of the artist Jemima Blackburn[14] and cousin (the son of his mother's brother) of the civil engineer William Dyce Cay. They were close friends and Cay acted as his best man when Maxwell married.[15]

Maxwell's parents did not meet and marry until they were well into their thirties;[16] his mother was nearly 40 years old when he was born. They had had one earlier child, a daughter named Elizabeth, who died in infancy.[17]

When Maxwell was young his family moved to Glenlair House, which his parents had built on the 1,500 acres (610 ha) Middlebie estate.[18] All indications suggest that Maxwell had maintained an unquenchable curiosity from an early age.[19] By the age of three, everything that moved, shone, or made a noise drew the question: "what's the go o' that?"[20] In a passage added to a letter from his father to his sister-in-law Jane Cay in 1834, his mother described this innate sense of inquisitiveness:

He is a very happy man, and has improved much since the weather got moderate; he has great work with doors, locks, keys, etc., and "show me how it doos" is never out of his mouth. He also investigates the hidden course of streams and bell-wires, the way the water gets from the pond through the wall....[21]

Education, 1839–47

Recognising the potential of the young boy, Maxwell's mother Frances took responsibility for James's early education, which in the Victorian era was largely the job of the woman of the house.[22] At eight he could recite long passages of Milton and the whole of the 119th psalm (176 verses). Indeed, his knowledge of scripture was already very detailed; he could give chapter and verse for almost any quotation from the psalms. His mother was taken ill with abdominal cancer and, after an unsuccessful operation, died in December 1839 when he was eight years old. James's education was then overseen by his father and his father's sister-in-law Jane, both of whom played pivotal roles in his life.[22] His formal schooling began unsuccessfully under the guidance of a sixteen-year-old hired tutor. Little is known about the young man John hired to instruct his son, except that he treated the younger boy harshly, chiding him for being slow and wayward.[22] John dismissed the tutor in November 1841 and, after considerable thought, sent James to the prestigious Edinburgh Academy.[23] He lodged during term times at the house of his aunt Isabella. During this time his passion for drawing was encouraged by his older cousin Jemima.[24]

Edinburgh Academy, where Maxwell was schooled.

The ten-year-old Maxwell, having been raised in isolation on his father's countryside estate, did not fit in well at school.[25] The first year had been full, obliging him to join the second year with classmates a year his senior.[25] His mannerisms and Galloway accent struck the other boys as rustic. Having arrived on his first day of school wearing a pair of homemade shoes and a tunic, he earned the unkind nickname of "Daftie".[26] He never seemed to resent the epithet, bearing it without complaint for many years.[27] Social isolation at the Academy ended when he met Lewis Campbell and Peter Guthrie Tait, two boys of a similar age who were to become notable scholars later in life. They remained lifelong friends.[10]

Maxwell was fascinated by geometry at an early age, rediscovering the regular polyhedra before he received any formal instruction.[24] Despite winning the school's scripture biography prize in his second year, his academic work remained unnoticed[24] until, at the age of 13, he won the school's mathematical medal and first prize for both English and poetry.[28]

Maxwell's interests ranged far beyond the school syllabus and he did not pay particular attention to examination performance.[28] He wrote his first scientific paper at the age of 14. In it he described a mechanical means of drawing mathematical curves with a piece of twine, and the properties of ellipses, Cartesian ovals, and related curves with more than two foci. His work Oval Curves was presented to the Royal Society of Edinburgh by James Forbes, a professor of natural philosophy at Edinburgh University,[10][29] but Maxwell was deemed too young to present the work himself.[30] The work was not entirely original, since René Descartes had also examined the properties of such multifocal ellipses in the seventeenth century, but he had simplified their construction.[30]

University of Edinburgh, 1847–50

Old College, University of Edinburgh

Maxwell left the Academy in 1847 at age 16 and began attending classes at the University of Edinburgh.[31] He had the opportunity to attend the University of Cambridge, but decided, after his first term, to complete the full course of his undergraduate studies at Edinburgh. The academic staff of Edinburgh University included some highly regarded names; his first year tutors included Sir William Hamilton, who lectured him on logic and metaphysics, Philip Kelland on mathematics, and James Forbes on natural philosophy.[10] He did not find his classes at Edinburgh University very demanding,[32] and was therefore able to immerse himself in private study during free time at the university and particularly when back home at Glenlair.[33] There he would experiment with improvised chemical, electric, and magnetic apparatus, but his chief concerns regarded the properties of polarised light.[34] He constructed shaped blocks of gelatine, subjected them to various stresses, and with a pair of polarising prisms given to him by William Nicol, viewed the coloured fringes that had developed within the jelly.[35] Through this practice he discovered photoelasticity, which is a means of determining the stress distribution within physical structures.[36]

At age 18, Maxwell contributed two papers for the Transactions of the Royal Society of Edinburgh. One of these, On the Equilibrium of Elastic Solids, laid the foundation for an important discovery later in his life, which was the temporary double refraction produced in viscous liquids by shear stress.[37] His other paper was Rolling Curves and, just as with the paper Oval Curves that he had written at the Edinburgh Academy, he was again considered too young to stand at the rostrum to present it himself. The paper was delivered to the Royal Society by his tutor Kelland instead.[38]

University of Cambridge, 1850–56

A young Maxwell at Trinity College, Cambridge. He is holding one of his colour wheels.

In October 1850, already an accomplished mathematician, Maxwell left Scotland for the University of Cambridge. He initially attended Peterhouse, but before the end of his first term transferred to Trinity, where he believed it would be easier to obtain a fellowship.[39] At Trinity he was elected to the elite secret society known as the Cambridge Apostles.[40] Maxwell's intellectual understanding of his Christian faith and of science grew rapidly during his Cambridge years. He joined the "Apostles", an exclusive debating society of the intellectual elite, where through his essays he sought to work out this understanding.

Now my great plan, which was conceived of old, ... is to let nothing be wilfully left unexamined. Nothing is to be holy ground consecrated to Stationary Faith, whether positive or negative. All fallow land is to be ploughed up and a regular system of rotation followed. ... Never hide anything, be it weed or no, nor seem to wish it hidden. ... Again I assert the Right of Trespass on any plot of Holy Ground which any man has set apart. ... Now I am convinced that no one but a Christian can actually purge his land of these holy spots. ... I do not say that no Christians have enclosed places of this sort. Many have a great deal, and every one has some. But there are extensive and important tracts in the territory of the Scoffer, the Pantheist, the Quietist, Formalist, Dogmatist, Sensualist, and the rest, which are openly and solemnly Tabooed. ..."

Christianity — that is, the religion of the Bible — is the only scheme or form of belief which disavows any possessions on such a tenure. Here alone all is free. You may fly to the ends of the world and find no God but the Author of Salvation. You may search the Scriptures and not find a text to stop you in your explorations. ...

The Old Testament and the Mosaic Law and Judaism are commonly supposed to be "Tabooed" by the orthodox. Sceptics pretend to have read them, and have found certain witty objections ... which too many of the orthodox unread admit, and shut up the subject as haunted. But a Candle is coming to drive out all Ghosts and Bugbears. Let us follow the light.''[41]

The extent to which Maxwell "ploughed up" his Christian beliefs and put them to the intellectual test, can be judged only incompletely from his writings. But there is plenty of evidence, especially from his undergraduate days, that he did deeply examine his faith. Certainly, his knowledge of the Bible was remarkable, so his confidence in the Scriptures was not based on ignorance.

In the summer of his third year, Maxwell spent some time at the Suffolk home of the Rev C.B. Tayler, the uncle of a class-mate, G.W.H. Tayler. The love of God shown by the family impressed Maxwell, particularly after he was nursed back from ill health by the minister and his wife.[42]

On his return to Cambridge, Maxwell writes to his recent host a chatty and affectionate letter including the following testimony,

... I have the capacity of being more wicked than any example that man could set me, and ... if I escape, it is only by God's grace helping me to get rid of myself, partially in science, more completely in society, — but not perfectly except by committing myself to God ...[41]

In November 1851, Maxwell studied under William Hopkins, whose success in nurturing mathematical genius had earned him the nickname of "senior wrangler-maker".[43]

In 1854, Maxwell graduated from Trinity with a degree in mathematics. He scored second highest in the final examination, coming behind Edward Routh and earning himself the title of Second Wrangler. He was later declared equal with Routh in the more exacting ordeal of the Smith's Prize examination.[44] Immediately after earning his degree, Maxwell read his paper On the Transformation of Surfaces by Bending to the Cambridge Philosophical Society.[45] This is one of the few purely mathematical papers he had written, demonstrating Maxwell's growing stature as a mathematician.[46] Maxwell decided to remain at Trinity after graduating and applied for a fellowship, which was a process that he could expect to take a couple of years.[47] Buoyed by his success as a research student, he would be free, apart from some tutoring and examining duties, to pursue scientific interests at his own leisure.[47]

The nature and perception of colour was one such interest which he had begun at Edinburgh University while he was a student of Forbes.[48] With the coloured spinning tops invented by Forbes, Maxwell was able to demonstrate that white light would result from a mixture of red, green, and blue light.[48] His paper Experiments on Colour laid out the principles of colour combination and was presented to the Royal Society of Edinburgh in March 1855.[49] Maxwell was this time able to deliver it himself.[49]

Maxwell was made a fellow of Trinity on 10 October 1855, sooner than was the norm,[49] and was asked to prepare lectures on hydrostatics and optics and to set examination papers.[50] The following February he was urged by Forbes to apply for the newly vacant Chair of Natural Philosophy at Marischal College, Aberdeen.[51] His father assisted him in the task of preparing the necessary references, but died on 2 April at Glenlair before either knew the result of Maxwell's candidacy.[51] Maxwell accepted the professorship at Aberdeen, leaving Cambridge in November 1856.[50]

Marischal College, Aberdeen, 1856–60

Maxwell proved that the Rings of Saturn were made of numerous small particles.

The 25-year-old Maxwell was a good fifteen years younger than any other professor at Marischal. He engaged himself with his new responsibilities as head of a department, devising the syllabus and preparing lectures.[52] He committed himself to lecturing 15 hours a week, including a weekly pro bono lecture to the local working men's college.[52] He lived in Aberdeen during the six months of the academic year and spent the summers at Glenlair, which he had inherited from his father.[13]

James and Katherine Maxwell, 1869

He focused his attention on a problem that had eluded scientists for two hundred years: the nature of Saturn's rings. It was unknown how they could remain stable without breaking up, drifting away or crashing into Saturn.[53] The problem took on a particular resonance at that time because St John's College, Cambridge had chosen it as the topic for the 1857 Adams Prize.[54] Maxwell devoted two years to studying the problem, proving that a regular solid ring could not be stable, while a fluid ring would be forced by wave action to break up into blobs. Since neither was observed, Maxwell concluded that the rings must be composed of numerous small particles he called "brick-bats", each independently orbiting Saturn.[54] Maxwell was awarded the £130 Adams Prize in 1859 for his essay On the stability of the motion of Saturn's rings;[55] he was the only entrant to have made enough headway to submit an entry.[56] His work was so detailed and convincing that when George Biddell Airy read it he commented "It is one of the most remarkable applications of mathematics to physics that I have ever seen."[57] It was considered the final word on the issue until direct observations by the Voyager flybys of the 1980s confirmed Maxwell's prediction.[58]

In 1857 Maxwell befriended the Reverend Daniel Dewar, who was then the Principal of Marischal.[59] Through him Maxwell met Dewar's daughter, Katherine Mary Dewar. They were engaged in February 1858 and married in Aberdeen on 2 June 1858. On the marriage record, Maxwell is listed as Professor of Natural Philosophy in Marischal College, Aberdeen.[60] Seven years Maxwell's senior, comparatively little is known of Katherine, although it is known that she helped in his lab and worked on experiments in viscosity.[61] Maxwell's biographer and friend, Lewis Campbell, adopted an uncharacteristic reticence on the subject of Katherine, though describing their married life as "one of unexampled devotion".[62]

In 1860 Marischal College merged with the neighbouring King's College to form the University of Aberdeen. There was no room for two professors of Natural Philosophy, so Maxwell, despite his scientific reputation, found himself laid off. He was unsuccessful in applying for Forbes's recently vacated chair at Edinburgh, the post instead going to Tait. Maxwell was granted the Chair of Natural Philosophy at King's College, London, instead.[63] After recovering from a near-fatal bout of smallpox in 1860, Maxwell moved to London with his wife.[64]

King's College, London, 1860–65

Commemoration of Maxwell's equations at King's College. One of three identical IEEE Milestone Plaques, the others being at Maxwell's birthplace in Edinburgh and the family home at Glenlair.[65]

Maxwell's time at King's was probably the most productive of his career. He was awarded the Royal Society's Rumford Medal in 1860 for his work on colour and was later elected to the Society in 1861.[66] This period of his life would see him display the world's first light-fast colour photograph, further develop his ideas on the viscosity of gases, and propose a system of defining physical quantities—now known as dimensional analysis. Maxwell would often attend lectures at the Royal Institution, where he came into regular contact with Michael Faraday. The relationship between the two men could not be described as being close, because Faraday was 40 years Maxwell's senior and showed signs of senility. They nevertheless maintained a strong respect for each other's talents.[67]

Blue plaque, 16 Palace Gardens Terrace, Kensington, Maxwell's home, 1860-65

This time is especially noteworthy for the advances Maxwell made in the fields of electricity and magnetism. He examined the nature of both electric and magnetic fields in his two-part paper On physical lines of force, which was published in 1861. In it he provided a conceptual model for electromagnetic induction, consisting of tiny spinning cells of magnetic flux. Two more parts were later added to and published in that same paper in early 1862. In the first additional part he discussed the nature of electrostatics and displacement current. In the second additional part, he dealt with the rotation of the plane of the polarisation of light in a magnetic field, a phenomenon that had been discovered by Faraday and is now known as the Faraday effect.[68]

Later years, 1865–1879

The gravestone at Parton Kirk (Galloway) of James Clerk Maxwell, his parents and his wife
This memorial stone to James Clerk Maxwell stands on a green in front of the church, beside the war memorial at Parton (Galloway).

In 1865 Maxwell resigned the chair at King's College, London, and returned to Glenlair with Katherine. In his paper On reciprocal figures, frames and diagrams of forces (1870) he discussed the rigidity of various designs of lattice.[69][70] He wrote the textbook Theory of Heat (1871) and the treatise Matter and Motion (1876). Maxwell was also the first to make explicit use of dimensional analysis, in 1871.[71]

In 1871 he became the first Cavendish Professor of Physics at Cambridge.[72] Maxwell was put in charge of the development of the Cavendish Laboratory, supervising every step in the progress of the building and of the purchase of the collection of apparatus.[73] One of Maxwell's last great contributions to science was the editing (with copious original notes) of the research of Henry Cavendish, from which it appeared that Cavendish researched, amongst other things, such questions as the density of the Earth and the composition of water.[74]

Maxwell died in Cambridge of abdominal cancer on 5 November 1879 at the age of 48.[31] His mother had died at the same age of the same type of cancer.[75] The minister who regularly visited him in his last weeks was astonished at his lucidity and the immense power and scope of his memory, but comments more particularly,

... his illness drew out the whole heart and soul and spirit of the man: his firm and undoubting faith in the Incarnation and all its results; in the full sufficiency of the Atonement; in the work of the Holy Spirit. He had gauged and fathomed all the schemes and systems of philosophy, and had found them utterly empty and unsatisfying — "unworkable" was his own word about them — and he turned with simple faith to the Gospel of the Saviour.

As death approached Maxwell told a Cambridge colleague

I have been thinking how very gently I have always been dealt with. I have never had a violent shove all my life. The only desire which I can have is like David to serve my own generation by the will of God, and then fall asleep.[41]

Maxwell is buried at Parton Kirk, near Castle Douglas in Galloway close to where he grew up.[76] The extended biography The Life of James Clerk Maxwell, by his former schoolfellow and lifelong friend Professor Lewis Campbell, was published in 1882.[77][78] His collected works were issued in two volumes by the Cambridge University Press in 1890.[79]

Personality

As a great lover of Scottish poetry, Maxwell memorised poems and wrote his own.[80] The best known is Rigid Body Sings, closely based on Comin' Through the Rye by Robert Burns, which he apparently used to sing while accompanying himself on a guitar. It has the opening lines[81]

Gin a body meet a body

Flyin' through the air.
Gin a body hit a body,
Will it fly? And where?

A collection of his poems was published by his friend Lewis Campbell in 1882.[82] Descriptions of Maxwell remark upon his remarkable intellectual qualities being matched by social awkwardness.[83]

Maxwell was an evangelical Presbyterian and in his later years became an Elder of the Church of Scotland.[84] Maxwell's religious beliefs and related activities have been the focus of a number of papers.[85][86][87][88] Attending both Church of Scotland (his father's denomination) and Episcopalian (his mother's denomination) services as a child, Maxwell later underwent an evangelical conversion in April 1853. One facet of this conversion may have aligned him with an antipositivist position.[87]

Scientific legacy

Electromagnetism

A postcard from Maxwell to Peter Tait.

Maxwell had studied and commented on electricity and magnetism as early as 1855 when his paper On Faraday's lines of force was read to the Cambridge Philosophical Society.[89] The paper presented a simplified model of Faraday's work and how the two phenomena were related. He reduced all of the current knowledge into a linked set of differential equations with 20 equations in 20 variables. This work was later published as On physical lines of force in March 1861.[90]

Around 1862, while lecturing at King's College, Maxwell calculated that the speed of propagation of an electromagnetic field is approximately that of the speed of light. He considered this to be more than just a coincidence, commenting, "We can scarcely avoid the conclusion that light consists in the transverse undulations of the same medium which is the cause of electric and magnetic phenomena."[57]

Working on the problem further, Maxwell showed that the equations predict the existence of waves of oscillating electric and magnetic fields that travel through empty space at a speed that could be predicted from simple electrical experiments; using the data available at the time, Maxwell obtained a velocity of 310,740,000 metres per second (1.0195×109 ft/s).[91] In his 1864 paper A dynamical theory of the electromagnetic field, Maxwell wrote, "The agreement of the results seems to show that light and magnetism are affections of the same substance, and that light is an electromagnetic disturbance propagated through the field according to electromagnetic laws".[6]

His famous equations, in their modern form of four partial differential equations, first appeared in fully developed form in his textbook A Treatise on Electricity and Magnetism in 1873.[92] Most of this work was done by Maxwell at Glenlair during the period between holding his London post and his taking up the Cavendish chair.[57] Maxwell expressed electromagnetism in the algebra of quaternions and made the electromagnetic potential the centrepiece of his theory.[93] In 1881 Oliver Heaviside replaced Maxwell's electromagnetic potential field by 'force fields' as the centrepiece of electromagnetic theory. Heaviside reduced the complexity of Maxwell's theory down to four differential equations, known now collectively as Maxwell's Laws or Maxwell's equations. According to Heaviside, the electromagnetic potential field was arbitrary and needed to be "murdered".[94] The use of scalar and vector potentials is now standard in the solution of Maxwell's equations.[95]

A few years later there was a debate between Heaviside and Peter Guthrie Tait about the relative merits of vector analysis and quaternions. The result was the realisation that there was no need for the greater physical insights provided by quaternions if the theory was purely local, and vector analysis became commonplace.[96] Maxwell was proven correct, and his quantitative connection between light and electromagnetism is considered one of the great accomplishments of 19th century mathematical physics.[97]

Maxwell also introduced the concept of the electromagnetic field in comparison to force lines that Faraday described.[98] By understanding the propagation of electromagnetism as a field emitted by active particles, Maxwell could advance his work on light. At that time, Maxwell believed that the propagation of light required a medium for the waves, dubbed the luminiferous aether.[98] Over time, the existence of such a medium, permeating all space and yet apparently undetectable by mechanical means, proved impossible to reconcile with experiments such as the Michelson–Morley experiment.[99] Moreover, it seemed to require an absolute frame of reference in which the equations were valid, with the distasteful result that the equations changed form for a moving observer. These difficulties inspired Albert Einstein to formulate the theory of special relativity; in the process Einstein dispensed with the requirement of a stationary luminiferous aether.[100]

Colour vision

First durable colour photographic image, demonstrated by James Clerk Maxwell in an 1861 lecture

As most physicists of the time, Maxwell had a strong interest in psychology. He was particularly interested, following the steps of Isaac Newton and Thomas Young, in the study of colour vision. From 1855 to 1872, he published at intervals a series of investigations concerning the perception of colour, colour-blindness, and colour theory, and was awarded the Rumford Medal for On the Theory of Colour Vision.[101]

Isaac Newton had demonstrated, using prisms, that white lights, such as sunlight, are composed of a number of monochromatic components which could then be recombined into white light.[102] However, Newton also showed that an orange paint made of yellow and red could look exactly like a monochromatic orange light, although being composed of two monochromatic yellow and red lights. Hence the paradox that puzzled physicists of the time: two complex lights (composed of more than one monochromatic light) could look alike but be physically different, called metameres. Thomas Young later proposed that this paradox could be explained by colours being perceived through a limited number of channels in the eyes, which he proposed to be threefold,[103] the trichromatic color theory. Maxwell used the recently developed Linear algebra to prove Young's theory. Any monochromatic light stimulating three receptors should be able to be equally stimulated by a set of three different monochromatic lights (in fact, by any set of three different lights). He demonstrated that to be the case,[104] inventing color matching experiments and Colorimetry.

Maxwell was also interested in applying his theory of color perception, namely in colour photography. Stemming directly from his psychological work on colour perception: if a sum of any three lights could reproduce any perceivable colour, then colour photographs could be produced with a set of three colored filters. In the course of his 1855 paper, Maxwell proposed that, if three black-and-white photographs of a scene were taken through red, green and blue filters and transparent prints of the images were projected onto a screen using three projectors equipped with similar filters, when superimposed on the screen the result would be perceived by the human eye as a complete reproduction of all the colours in the scene.[105]

During an 1861 Royal Institution lecture on colour theory, Maxwell presented the world's first demonstration of colour photography by this principle of three-colour analysis and synthesis. Thomas Sutton, inventor of the single-lens reflex camera, did the actual picture-taking. He photographed a tartan ribbon three times, through red, green, and blue filters, also making a fourth photograph through a yellow filter, which, according to Maxwell's account, was not used in the demonstration. Because Sutton's photographic plates were insensitive to red and barely sensitive to green, the results of this pioneering experiment were far from perfect. It was remarked in the published account of the lecture that "if the red and green images had been as fully photographed as the blue," it "would have been a truly-coloured image of the riband. By finding photographic materials more sensitive to the less refrangible rays, the representation of the colours of objects might be greatly improved."[66][106][107] Researchers in 1961 concluded that the seemingly impossible partial success of the red-filtered exposure was due to ultraviolet light, which is strongly reflected by some red dyes, not entirely blocked by the red filter used, and within the range of sensitivity of the wet collodion process Sutton employed.[108]

Kinetic theory and thermodynamics

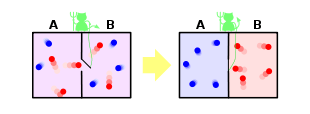
Maxwell's demon, a thought experiment where entropy decreases.

Maxwell also investigated the kinetic theory of gases. Originating with Daniel Bernoulli, this theory was advanced by the successive labours of John Herapath, John James Waterston, James Joule, and particularly Rudolf Clausius, to such an extent as to put its general accuracy beyond a doubt; but it received enormous development from Maxwell, who in this field appeared as an experimenter (on the laws of gaseous friction) as well as a mathematician.[109]

Between 1859 and 1866, he developed the theory of the distributions of velocities in particles of a gas, work later generalised by Ludwig Boltzmann.[110][111] The formula, called the Maxwell–Boltzmann distribution, gives the fraction of gas molecules moving at a specified velocity at any given temperature. In the kinetic theory, temperatures and heat involve only molecular movement. This approach generalised the previously established laws of thermodynamics and explained existing observations and experiments in a better way than had been achieved previously. Maxwell's work on thermodynamics led him to devise the thought experiment that came to be known as Maxwell's demon, where the second law of thermodynamics is violated by an imaginary being capable of sorting particles by energy.[112]

In 1871 he established Maxwell's thermodynamic relations, which are statements of equality among the second derivatives of the thermodynamic potentials with respect to different thermodynamic variables. In 1874, he constructed a plaster thermodynamic visualisation as a way of exploring phase transitions, based on the American scientist Josiah Willard Gibbs's graphical thermodynamics papers.[113][114]

Control theory

Main article: Control theory

Maxwell published a paper On governors in the Proceedings of Royal Society, vol. 16 (1867–1868).[115] This paper is considered a central paper of the early days of control theory.[116] Here "governors" refers to the governor or the centrifugal governor used to regulate steam engines.

Legacy

The James Clerk Maxwell Monument in Edinburgh. By Alexander Stoddart. Commissioned by The Royal Society of Edinburgh. Unveiled in 2008.

His name is honoured in several ways:

Publications

References

Notes

  1. ↑ "Mechanical conservation of energy / Maxwell's wheel" (PDF). PHYWE Laboratory Experiments: Physics. Retrieved 14 July 2014.
  2. ↑ "Early day motion 2048". UK Parliament. Retrieved 22 April 2013.
  3. ↑ "James Clerk Maxwell". The Science Museum, London. Retrieved 22 April 2013.
  4. ↑ "Topology and Scottish mathematical physics". University of St Andrews. Retrieved 9 September 2013.
  5. ↑ Nahin, P.J. (1992). "Maxwell's grand unification". Spectrum, IEEE 29 (3): 45. doi:10.1109/6.123329.
  6. 1 2 Maxwell, James Clerk (1865). "A dynamical theory of the electromagnetic field" (PDF). Philosophical Transactions of the Royal Society of London 155: 459–512. Bibcode:1865RSPT..155..459C. doi:10.1098/rstl.1865.0008. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society. His statement that "light and magnetism are affections of the same substance" is at page 499.)
  7. ↑ Tolstoy 1982, p. 2
  8. ↑ "Einstein the greatest". BBC News (BBC). 29 November 1999. Retrieved 2 April 2010.
  9. ↑ McFall, Patrick (23 April 2006). "Brainy young James wasn't so daft after all". The Sunday Post. maxwellyear2006.org. Retrieved 29 March 2013.
  10. 1 2 3 4 5 Harman 2004, p. 506
  11. ↑ Waterston & Macmillan Shearer 2006, p. 633
  12. ↑ Laidler, Keith James (2002). Energy and the Unexpected. Oxford University Press. p. 49. ISBN 9780198525165.
  13. 1 2 Maxwell, James Clerk (2011). "Preface". The Scientific Papers of James Clerk Maxwell. ISBN 9781108012256.
  14. ↑ "Jemima Blackburn". Gazetteer for Scotland. Retrieved 27 August 2013.
  15. ↑ "William Dyce Cay". scottisharchitects.org.uk.
  16. ↑ Tolstoy 1982, p. 11
  17. ↑ Campbell 1882, p. 1
  18. ↑ Mahon 2003, pp. 186–7
  19. ↑ Tolstoy 1982, p. 13
  20. ↑ Mahon 2003, p. 3
  21. ↑ Campbell 1882, p. 27
  22. 1 2 3 Tolstoy 1982, pp. 15–16
  23. ↑ Campbell 1882, pp. 19–21
  24. 1 2 3 Mahon 2003, pp. 12–14
  25. 1 2 Mahon 2003, p. 10
  26. ↑ Mahon 2003, p. 4
  27. ↑ Campbell 1882, pp. 23–24
  28. 1 2 Campbell 1882, p. 43
  29. ↑ Gardner 2007, pp. 46–49
  30. 1 2 Mahon 2003, p. 16
  31. 1 2 Harman 2004, p. 662
  32. ↑ Tolstoy 1982, p. 46
  33. ↑ Campbell 1882, p. 64
  34. ↑ Mahon 2003, pp. 30–31
  35. ↑ Timoshenko 1983, p. 58
  36. ↑ Russo 1996, p. 73
  37. ↑ Timoshenko 1983, pp. 268–278
  38. ↑ Glazebrook 1896, p. 23
  39. ↑ Glazebrook 1896, p. 28
  40. ↑ Glazebrook 1896, p. 30
  41. 1 2 3 "James Clerk Maxwell and the Christian Proposition". MIT IAP Seminar. Retrieved 13 October 2014.
  42. ↑ Campbell 1882, pp. 169–170
  43. ↑ Warwick 2003, pp. 84–85
  44. ↑ Tolstoy 1982, p. 62
  45. ↑ Harman 1998, p. 3
  46. ↑ Tolstoy 1982, p. 61
  47. 1 2 Mahon 2003, pp. 47–48
  48. 1 2 Mahon 2003, p. 51
  49. 1 2 3 Tolstoy 1982, pp. 64–65. The full title of Maxwell's paper was Experiments on colour, as perceived by the eye, with remarks on colour-blindness.
  50. 1 2 Glazebrook 1896, pp. 43–46
  51. 1 2 Campbell 1882, p. 126
  52. 1 2 Mahon 2003, pp. 69–71
  53. ↑ Harman 1998, pp. 48–53
  54. 1 2 Harman 2004, p. 508
  55. ↑ "On the stability of the motion of Saturn's rings" (PDF). Retrieved 24 March 2014.
  56. ↑ Mahon 2003, p. 75
  57. 1 2 3 O'Connor, J. J.; Robertson, E. F. (November 1997). "James Clerk Maxwell". School of Mathematical and Computational Sciences University of St Andrews. Retrieved 25 March 2013.
  58. ↑ "James Clerk Maxwell (1831–1879)". National Library of Scotland. Retrieved 27 August 2013.
  59. ↑ "Very Rev. Daniel Dewar DD (I20494)". Stanford University. Retrieved 27 August 2013.
  60. ↑ James Clerk Maxwell and Katherine Mary Dewar marriage certificate, Family History Library film #280176, district 168/2 (Old Machar, Aberdeen), page 83, certificate No. 65.
  61. ↑ Maxwell 2001, p. 351
  62. ↑ Tolstoy 1982, pp. 88–91
  63. ↑ Glazebrook 1896, p. 54
  64. ↑ Tolstoy 1982, p. 98
  65. ↑ "James Clerk Maxwell Foundation" (PDF). James Clerk Maxwell Foundation. Retrieved 28 May 2015.
  66. 1 2 Tolstoy 1982, p. 103
  67. ↑ Tolstoy 1982, pp. 100–1
  68. ↑ Mahon 2003, p. 109
  69. ↑ Maxwell, J. Clerk (2013). "I.—On Reciprocal Figures, Frames, and Diagrams of Forces". Transactions of the Royal Society of Edinburgh 26: 1. doi:10.1017/S0080456800026351.
  70. ↑ Crapo, Henry (1979). "Structural rigidity" (PDF). Structural Topology (1): 26–45.
  71. ↑ Lestienne, Rémy (1998). The Creative Power of Chance. pp. 20–21. ISBN 9780252066863.
  72. ↑ "The Cavendish Professorship of Physics". University of Cambridge, Department of Physics. Retrieved 27 March 2013.
  73. ↑ Moralee, Dennis. "The Old Cavendish – "The First Ten Years"". University of Cambridge Department of Physics. Retrieved 30 June 2013.
  74. ↑ Jones, Roger (2009). What's Who?: A Dictionary of Things Named After People and the People They are Named After. p. 40. ISBN 9781848760479.
  75. ↑ "James Clerk Maxwell Foundation" (PDF). Retrieved 30 June 2013.
  76. ↑ "Parton & Sam Callander". James Clerk Maxwell Foundation. Retrieved 30 June 2013.
  77. ↑ Campbell, Lewis (2010). The Life of James Clerk Maxwell: With a Selection from His Correspondence and Occasional Writings and a Sketch of His Contributions to Science. ISBN 9781108013703.
  78. ↑ Campbell, Lewis (1882). The Life of James Clerk Maxwell: With a Selection from His Correspondence and Occasional Writings and a Sketch of His Contributions to Science (1 ed.). London: Macmillan. Retrieved 16 June 2014.
  79. ↑ Maxwell, James Clerk (2011). The Scientific Papers of James Clerk Maxwell. ISBN 9781108012256.
  80. ↑ Seitz, Frederick. "James Clerk Maxwell (1831–1879); Member APS 1875" (PDF). Philadelphia: The American Philosophical Society. Retrieved 20 May 2011.
  81. ↑ "Rigid Body Sings". Haverford College. Retrieved 26 March 2013.
  82. ↑ "Selected Poetry of James Clerk Maxwell (1831–1879)". University of Toronto Libraries. Retrieved 27 August 2013.
  83. ↑ Klein, Maury (2010). The Power Makers: Steam, Electricity, and the Men Who Invented Modern America. p. 88. ISBN 9781596918344.
  84. ↑ "The Aberdeen university review". The Aberdeen University Review (The Aberdeen University Press) III. 1916.
  85. ↑ Jerrold, L. McNatt (3 September 2004). "James Clerk Maxwell's Refusal to Join the Victoria Institute" (PDF). American Scientific Affiliation. Retrieved 25 March 2013.
  86. ↑ Marston, Philip L. (2007). "Maxwell and creation: Acceptance, criticism, and his anonymous publication". American Journal of Physics 75 (8): 731–740. Bibcode:2007AmJPh..75..731M. doi:10.1119/1.2735631.
  87. 1 2 Theerman, Paul (1986). "James Clerk Maxwell and religion". American Journal of Physics 54 (4): 312–317. Bibcode:1986AmJPh..54..312T. doi:10.1119/1.14636.
  88. ↑ Hutchinson, Ian (2006) [January 1998]. "James Clerk Maxwell and the Christian Proposition". Retrieved 26 March 2013.
  89. ↑ Maxwell, James Clerk (1855). "On Faraday's Lines of Force". Transactions of the Cambridge Philosophical Society. blazelabs.com. Retrieved 27 March 2013.
  90. ↑ "1861: James Clerk Maxwell's greatest year". King's College London. 18 April 2011. Retrieved 28 March 2013.
  91. ↑ "ECEN3410 Electromagnetic Waves" (PDF). University of Colorado. Retrieved 30 June 2013.
  92. ↑ "Year 13 – 1873: A Treatise on Electricity and Magnetism by James Clerk Maxwell". MIT Libraries. Retrieved 30 June 2013.
  93. ↑ "Extraordinary Physics". The Tom Bearden Website. Retrieved 30 April 2013.
  94. ↑ Hunt, B. J. (1984). The Maxwellians (PhD). The Johns Hopkins University. pp. 116–117.
  95. ↑ Eyges 1972, p. section 11.6.
  96. ↑ Barrett & Grimes 1995, pp. 7–8
  97. ↑ Wheen, Andrew (2010). Dot-Dash to Dot.Com: How Modern Telecommunications Evolved from the Telegraph to the Internet. p. 86. ISBN 9781441967602.
  98. 1 2 Johnson, Kevin (May 2002). "The Electromagnetic Field". University of St Andrews. Retrieved 30 June 2013.
  99. ↑ Michelson, Albert Abraham; Morley, Edward Williams (1887). "On the Relative Motion of the Earth and the Luminiferous Ether". American Journal of Science 34 (203): 333–345. doi:10.2475/ajs.s3-34.203.333.
  100. ↑ Einstein, Albert. "Ether and the Theory of Relativity". Retrieved 19 December 2013.
  101. ↑ Johnson, Kevin (May 2012). "Colour Vision". University of St Andrews. Retrieved 20 May 2013.
  102. ↑ Newton, Isaac (1704). Opticks: or a treatise of the reflexions, refractions, inflexions and colours of light. London: Printed for Sam. Smith, and Benj. Walford, Printers to the Royal Society, at the Prince's Arms in St. Paul's Church-yard.
  103. ↑ Young, Thomas (1804). "Bakerian Lecture: Experiments and calculations relative to physical optics". Philosophical Transactions of the Royal Society 94: 1–16. Bibcode:1804RSPT...94....1Y. doi:10.1098/rstl.1804.0001.
  104. ↑ Maxwell, James (1857). "XVIII.—Experiments on Colour, as perceived by the Eye, with Remarks on Colour-Blindness". Transactions of the Royal Society of Edinburgh (Royal Society of Edinburgh) 21 (02): 275–298. |first2= missing |last2= in Authors list (help)
  105. ↑ Maxwell, James Clerk (1855). "Experiments on Colour, as Perceived by the Eye, with Remarks on Colour-Blindness". Transactions of the Royal Society of Edinburgh 21 (2): 275–298. doi:10.1017/S0080456800032117. (This thought-experiment is described on pages 283–284. The short-wavelength filter is specified as "violet", but during the 19th century "violet" could be used to describe a deep violet-blue such as the colour of cobalt glass.)
  106. ↑ Maxwell, J. Clerk (2011) [1890]. "On the Theory of Three Primary Colours". The Scientific Papers of James Clerk Maxwell 1. Cambridge University Press. pp. 445–450. ISBN 9780511698095. Retrieved 28 March 2013.
  107. ↑ Maxwell, J. Clerk (1861). "The Theory of the Primary Colours". The British Journal of Photography. Retrieved 28 March 2013.
  108. ↑ Evans, R. (November 1961). "Maxwell's Color Photography". Scientific American 205 (5): 117–128. doi:10.1038/scientificamerican1161-118.
  109. ↑ "Archives Biographies: James Clerk Maxwell". The Institution of Engineering and Technology. Retrieved 1 July 2013.
  110. ↑ Hill, Melanie. "The Maxwell–Boltzmann distribution" (PDF). Georgia Institute of Technology. Retrieved 28 August 2013.
  111. ↑ Xiang, Hong Wei (2005). The Corresponding-States Principle and its Practice: Thermodynamic, Transport and Surface Properties of Fluids. p. 51. ISBN 9780080459042.
  112. ↑ Edwards, Lin (15 November 2010). "Maxwell's demon demonstration turns information into energy". phys.org. Retrieved 1 July 2013.
  113. ↑ West, Thomas G. (February 1999). "James Clerk Maxwell, Working in Wet Clay". SIGGRAPH Computer Graphics Newsletter 33 (1): 15–17. doi:10.1145/563666.563671.
  114. ↑ Cropper, William H. (2004). Great Physicists: The Life and Times of Leading Physicists from Galileo to Hawking. Oxford University Press. p. 118. ISBN 9780195173246.
  115. ↑ Maxwell, James Clerk (1868). "On Governors". Proceedings of the Royal Society of London 16: 270–283. doi:10.1098/rspl.1867.0055. JSTOR 112510.
  116. ↑ Mayr, Otto (1971). "Maxwell and the Origins of Cybernetics". Isis 62 (4): 424–444. doi:10.1086/350788.
  117. 1 2 3 "James Clerk Maxwell". martinfrost.ws. Retrieved 30 June 2013.
  118. ↑ "PIA09857: Maxwell's Namesake". JPL/NASA. Retrieved 1 July 2013.
  119. ↑ "James Clerk Maxwell Building (JCMB)". University of Edinburgh. Retrieved 1 July 2013.
  120. ↑ "James Clerk Maxwell". King's College London. Retrieved 1 July 2013.
  121. ↑ "James Clerk Maxwell Science Centre". Edinburgh Academy. Retrieved 30 June 2013.
  122. ↑ Rinaldi, Giancarlo (25 November 2008). "The science world's unsung hero?". BBC. Retrieved 27 March 2013.
  123. ↑ Shilov, Anton (29 August 2014). "Nvidia to skip GeForce GTX 800 series, to introduce GeForce GTX 970, GTX 980 in mid-September". KitGuru.

Bibliography

External links

Wikimedia Commons has media related to James Clerk Maxwell.
Wikiquote has quotations related to: James Clerk Maxwell
Wikisource has original works written by or about:
James Clerk Maxwell
This article is issued from Wikipedia - version of the Monday, February 15, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.