Jacobi set
In Morse theory, a mathematical discipline, Jacobi sets provide a method of studying the relationship between two or more Morse functions.
For two Morse functions, the Jacobi set is defined as the set of critical points of the restriction of one function to the level sets of the other function.[1]
The Jacobi set can also be defined as the set of points where the gradients of the two functions are parallel.
If both the functions are generic, the Jacobi set is a smoothly embedded 1-manifold.
Definition
Consider two generic Morse functions 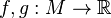 defined on a smooth
defined on a smooth 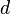 -manifold. Let the restriction of
-manifold. Let the restriction of  to the level set
to the level set 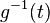 for
for 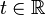 a regular value, be called
a regular value, be called 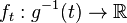 ; it is a Morse function. Then the Jacobi set
; it is a Morse function. Then the Jacobi set 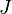 of
of  and
and  is
is 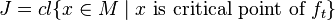 ,
,
Alternatively, the Jacobi set is the collection of points where the gradients of the functions align with each other or one of the gradients vanish (cite?), for some 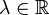 ,
,
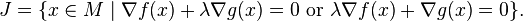
Equivalently, the Jacobi set can be described as the collection of critical points of the family of functions 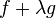 , for some
, for some 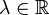 ,
,
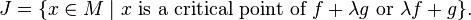
References
- ↑ Edelsbrunner, Herbert; John Harer (2002). "Jacobi sets of multiple morse functions". Foundations of Computational Mathematics (Cambridge University Press): 37–57.