Isotypical representation

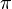In group theory, an isotypical or primary representation of a group G is a unitary representation $\pi : G \longrightarrow \mathcal{B}(\mathcal{H})$ such that any two subrepresentations have equivalent subsubrepresentations. This is related to the notion of a primary or factor representation of a C*-algebra, or to the factor for a von Neumann algebra: the representation $\pi$ of G is isotypical iff 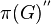$\pi(G)^{''}$ is a factor.

This term more generally used in the context of semisimple modules.

Property

One of the interesting property of this notion lies in the fact that two isotypical representations are either quasi-equivalent or disjoint (in analogy with the fact that irreducible representations are either unitarily equivalent or disjoint).

This can be understood through the correspondence between factor representations and minimal central projection (in a von Neumann algebra),.^[1] Two minimal central projections are then either equal or orthogonal.

Example

Let G be a compact group. A corollary of the Peter–Weyl theorem has that any unitary representation $\pi : G \longrightarrow \mathcal{B}(\mathcal{H})$ on a separable Hilbert space $\mathcal{H}$ is a possibly infinite direct sum of finite dimensional irreducible representations. An isotypical representation is any direct sum of equivalent irreducible representations that appear (typically multiple times) in $\mathcal{H}$ .

References

↑ Dixmier C*-algebras Prop. 5.2.7 p.117 1977

Mackey
"C* algebras", Jacques Dixmier, Chapter 5
"Lie Groups", Claudio Procesi, def. p. 156.
"Group and symmetries", Yvette Kosmann-Schwarzbach

This article is issued from Wikipedia - version of the Sunday, October 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.