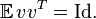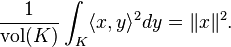Isotropic position
In the fields of machine learning, the theory of computation, and random matrix theory, a probability distribution over vectors is said to be in isotropic position if its covariance matrix is equal to the identity matrix.
Formal definitions
Let 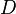 be a distribution over vectors in the vector space
be a distribution over vectors in the vector space 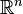 .
Then
.
Then 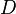 is in isotropic position if, for vector
is in isotropic position if, for vector 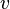 sampled from the distribution,
sampled from the distribution,
A set of vectors is said to be in isotropic position if the uniform distribution over that set is in isotropic position. In particular, every orthonormal set of vectors is isotropic.
As a related definition, a convex body 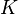 in
in 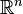 is in isotropic position if, for all vectors
is in isotropic position if, for all vectors 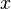 in
in 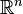 , we have
, we have
See also
References
- Rudelson, M. (1999). "Random Vectors in the Isotropic Position". Journal of Functional Analysis 164 (1): 60–72. arXiv:math/9608208.
This article is issued from Wikipedia - version of the Sunday, January 03, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.