Isotomic conjugate
In geometry, the isotomic conjugate of a point P with respect to a triangle ABC is another point, defined from P and ABC.
Construction
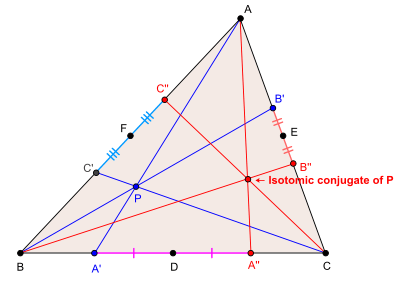
We assume that P is not collinear with any two vertices of ABC. Let A', B' and C' be the points in which the lines AP, BP, CP meet sidelines BC, CA and AB (extended if necessary). Reflecting A', B', C' in the midpoints of sides BC, CA, AB will give points A", B" and C" respectively. The isotomic lines AA", BB" and CC" joining these new points to the vertices meet at a point (which can be proved using Ceva's theorem), the isotomic conjugate of P.
Coordinates
If trilinears for P are p : q : r, then trilinears for the isotomic conjugate of P are
- a−2p−1 : b−2q−1 : c−2r−1.
Properties
The isotomic conjugate of the centroid of triangle ABC is the centroid itself.
The isotomic conjugate of the symmedian point is the third Brocard point, and the isotomic conjugate of the Gergonne point is the Nagel point.
Isotomic conjugates of lines are circumconics, and conversely, isotomic conjugates of circumconics are lines. (This property holds for isogonal conjugates as well.)
References
- Robert Lachlan, An Elementary Treatise on Modern Pure Geometry, Macmillan and Co., 1893, page 57.