Isolated singularity
In complex analysis, a branch of mathematics, an isolated singularity is one that has no other singularities close to it. In other words, a complex number z0 is an isolated singularity of a function f if there exists an open disk D centered at z0 such that f is holomorphic on D \ {z0}, that is, on the set obtained from D by taking z0 out.
Formally, and within the general scope of functional analysis, an isolated singularity for a function  is any topologically isolated point within an open set where the function is defined.
is any topologically isolated point within an open set where the function is defined.
Every singularity of a meromorphic function is isolated, but isolation of singularities is not alone sufficient to guarantee a function is meromorphic. Many important tools of complex analysis such as Laurent series and the residue theorem require that all relevant singularities of the function be isolated. There are three types of singularities: removable singularities, poles and essential singularities.
Examples
- The function
 has 0 as an isolated singularity.
has 0 as an isolated singularity.
Nonisolated singularities
Other than isolated singularities, complex functions of one variable may exhibit other singular behaviour. Namely, two kinds of nonisolated singularities exist:
- Cluster points, i.e. limit points of isolated singularities: if they are all poles, despite admitting Laurent series expansions on each of them, no such expansion is possible at its limit.
- Natural boundaries, i.e. any non-isolated set (e.g. a curve) which functions cannot be analytically continued around (or outside them if they are closed curves in the Riemann sphere).
Examples

- The function
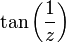 is meromorphic in
is meromorphic in  , with simple poles in
, with simple poles in 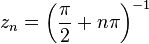 , for every
, for every 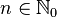 . Since
. Since 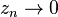 , every punctured disk centred in
, every punctured disk centred in  has an infinite number of singularities within, so no Laurent expansion is available for
has an infinite number of singularities within, so no Laurent expansion is available for 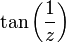 around
around  , which is in fact a cluster point of its poles.
, which is in fact a cluster point of its poles.
- The function
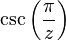 has a singularity at 0 which is not isolated, since there are additional singularities at the reciprocal of every integer which are located arbitrarily close to 0 (though the singularities at these reciprocals are themselves isolated).
has a singularity at 0 which is not isolated, since there are additional singularities at the reciprocal of every integer which are located arbitrarily close to 0 (though the singularities at these reciprocals are themselves isolated).
- The function here defined as the Maclaurin series
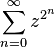 converges inside the open unit disk centred at
converges inside the open unit disk centred at  and has the unit circle as its natural boundary.
and has the unit circle as its natural boundary.
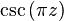 has every
has every