Ionic strength

The ionic strength of a solution is a measure of the concentration of ions in that solution. Ionic compounds, when dissolved in water, dissociate into ions. The total electrolyte concentration in solution will affect important properties such as the dissociation or the solubility of different salts. One of the main characteristics of a solution with dissolved ions is the ionic strength.

Quantifying ionic strength

The ionic strength, I, of a solution is a function of the concentration of all ions present in that solution.

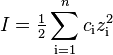
I = \begin{matrix}\frac{1}{2}\end{matrix}\sum_{{\rm i}=1}^{n} c_{\rm i}z_{\rm i}^{2}

where ci is the molar concentration of ion i (M, mol/L), zi is the charge number of that ion, and the sum is taken over all ions in the solution. For a 1:1 electrolyte such as sodium chloride, the ionic strength is equal to the concentration, but for MgSO4 the ionic strength is four times higher. Generally multivalent ions contribute strongly to the ionic strength.

Calculation example

For example the ionic strength of a mixed 0.050 M in Na2SO4 and 0.020 M in KCl solution is:

I = 1/2 × [(Concentration of Na2SO4 in M × # of Sodium ions × (Charge of Sodium)2) + (Concentration of Na2SO4 in M × # of SO4 ions × (Charge of SO4)2) + (Concentration of KCl × # of Potassium ions × (Charge of Potassium)2) + (Concentration of KCl in M × # of Chloride ions × (Charge of Chloride)2)]
I = 1/2 × [(0.050 M × 2 × (+1)2) + (0.050 M × 1 × (−2)2) + (0.020 M × 1 × (+1)2) + (0.020 M × 1 × (−1)2)] = 0.17 M

Non-ideal solutions

Because in non-ideal solutions volumes are no longer strictly additive it is often preferable to work with molality b (mol/kg{H2O}) rather than molarity c (mol/L). In that case, ionic strength is defined as:

I = \begin{matrix}\frac{1}{2}\end{matrix}\sum_{{i}=1}^{n} b_{i}z_{i}^{2}

in which

i = ion identification number
z = charge of ion

Importance

The ionic strength plays a central role in the Debye–Hückel theory that describes the strong deviations from ideality typically encountered in ionic solutions. It is also important for the theory of double layer and related electrokinetic phenomena and electroacoustic phenomena in colloids and other heterogeneous systems. That is, the Debye length, which is the inverse of the Debye parameter (κ), is inversely proportional to the square root of the ionic strength. Debye length is characteristic of the double layer thickness. Increasing the concentration or valence of the counterions compresses the double layer and increases the electrical potential gradient.

Media of high ionic strength are used in stability constant determination in order to minimize changes, during a titration, in the activity quotient of solutes at lower concentrations. Natural waters such as seawater have a non-zero ionic strength due to the presence of dissolved salts which significantly affects their properties.

See also

External links

References

This article is issued from Wikipedia - version of the Friday, January 15, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.