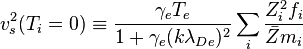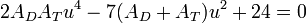Ion acoustic wave
In plasma physics, an ion acoustic wave is one type of longitudinal oscillation of the ions and electrons in a plasma, much like acoustic waves traveling in neutral gas. However, because the waves propagate through positively charged ions, ion acoustic waves can interact with their electromagnetic fields, as well as simple collisions. In plasmas, ion acoustic waves are frequently referred to as acoustic waves or even just sound waves. They commonly govern the evolution of mass density, for instance due to pressure gradients, on time scales longer than the frequency corresponding to the relevant length scale. Ion acoustic waves can occur in an unmagnetized plasma or in a magnetized plasma parallel to the magnetic field. For a single ion species plasma and in the long wavelength limit, the waves are dispersionless (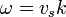 ) with a speed given by (see derivation below)
) with a speed given by (see derivation below)
where  is Boltzmann's constant,
is Boltzmann's constant,  is the mass of the ion,
is the mass of the ion, 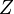 is its charge,
is its charge, 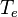 is the temperature of the electrons and
is the temperature of the electrons and 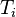 is the temperature of the ions. Normally γe is taken to be unity, on the grounds that the thermal conductivity of electrons is large enough to keep them isothermal on the time scale of ion acoustic waves, and γi is taken to be 3, corresponding to one-dimensional motion. In collisionless plasmas, the electrons are often much hotter than the ions, in which case the second term in the numerator can be ignored.
is the temperature of the ions. Normally γe is taken to be unity, on the grounds that the thermal conductivity of electrons is large enough to keep them isothermal on the time scale of ion acoustic waves, and γi is taken to be 3, corresponding to one-dimensional motion. In collisionless plasmas, the electrons are often much hotter than the ions, in which case the second term in the numerator can be ignored.
Derivation
We derive the ion acoustic wave dispersion relation for a linearized fluid description of a plasma with N ion species. A subscript 0 denotes constant equilibrium quantities, and 1 denotes first-order perturbations. We assume the pressure perturbations for each species (electrons and ions) are a Polytropic_process, namely 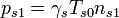 for species s. To justify this assumption and determine the value of
for species s. To justify this assumption and determine the value of 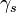 , one must use a kinetic treatment that solves for the species distribution functions in velocity space.
, one must use a kinetic treatment that solves for the species distribution functions in velocity space.
Using the ion continuity equation, the ion momentum equation becomes
We relate the electric field  to the electron density by the electron momentum equation:
to the electron density by the electron momentum equation:
We now neglect the left-hand side, which is due to electron inertia. This is valid for waves with frequencies much less than the electron plasma frequency. The resulting electric field is
Since we have already solved for the electric field, we cannot also find it from Poisson's equation. The ion momentum equation now relates 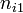 for each species to
for each species to  :
:
We arrive at a dispersion relation via Poisson's equation:
The first bracketed term on the right is zero by assumption (charge-neutral equilibrium). We substitute for the electric field and rearrange to find
 .
.
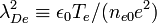 defines the electron Debye length. The second term on the left arises from the
defines the electron Debye length. The second term on the left arises from the 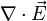 term, and reflects the degree to which the perturbation is not charge-neutral. If
term, and reflects the degree to which the perturbation is not charge-neutral. If 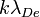 is small we may drop this term. This approximation is sometimes called the plasma approximation.
is small we may drop this term. This approximation is sometimes called the plasma approximation.
We now work in Fourier space, and find
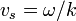 is the wave phase velocity. Substituting this into Poisson's equation gives us an expression where each term is proportional to
is the wave phase velocity. Substituting this into Poisson's equation gives us an expression where each term is proportional to  . To find the dispersion relation for natural modes, we look for solutions for
. To find the dispersion relation for natural modes, we look for solutions for  nonzero and find:
nonzero and find:
-
![\gamma_eT_e \sum_{i=1}^N Z_i^2f_i[m_iv_s^2-\gamma_iT_i]^{-1} = \bar Z(1+\gamma_ek^2\lambda_{De}^2)](../I/m/80a78cfb92a2fca93c37489f1fb9142a.png)
(dispgen)
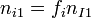 where
where 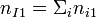 , and
, and  . A unitless version of this equation is
. A unitless version of this equation is
with 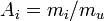 ,
, 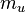 is the atomic mass unit,
is the atomic mass unit,  , and
, and
If 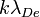 is small (the plasma approximation), we can neglect the second term on the right-hand side, and the wave is dispersionless
is small (the plasma approximation), we can neglect the second term on the right-hand side, and the wave is dispersionless 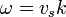 with
with  independent of k.
independent of k.
Dispersion Relation
The general dispersion relation given above for ion acoustic waves can be put in the form of an order-N polynomial (for N ion species) in 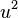 . All of the roots should be real-positive, since we have neglected damping. The two signs of
. All of the roots should be real-positive, since we have neglected damping. The two signs of 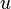 correspond to right- and left-moving waves. For a single ion species,
correspond to right- and left-moving waves. For a single ion species,
We now consider multiple ion species, for the common case 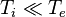 . For
. For  , the dispersion relation has N-1 degenerate roots
, the dispersion relation has N-1 degenerate roots  , and one non-zero root
, and one non-zero root
This non-zero root is called the "fast mode", since  is typically greater than all the ion thermal speeds. The approximate fast-mode solution for
is typically greater than all the ion thermal speeds. The approximate fast-mode solution for 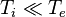 is
is
The N-1 roots that are zero for  are called "slow modes", since
are called "slow modes", since  can be comparable to or less than the thermal speed of one or more of the ion species.
can be comparable to or less than the thermal speed of one or more of the ion species.
A case of interest to nuclear fusion is an equimolar mixture of deuterium and tritium ions (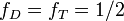 ). Let us specialize to full ionization (
). Let us specialize to full ionization ( ), equal temperatures (
), equal temperatures (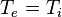 ), polytrope exponents
), polytrope exponents 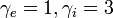 , and neglect the
, and neglect the  contribution. The dispersion relation becomes a quadratic in
contribution. The dispersion relation becomes a quadratic in  , namely:
, namely:
Using  we find the two roots are
we find the two roots are 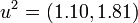 .
.
Another case of interest is one with two ion species of very different masses. An example is a mixture of gold (A=197) and boron (A=10.8), which is currently of interest in hohlraums for laser-driven inertial fusion research. For a concrete example, consider  and
and 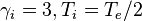 for both ion species, and charge states Z=5 for boron and Z=50 for gold. We leave the boron atomic fraction
for both ion species, and charge states Z=5 for boron and Z=50 for gold. We leave the boron atomic fraction 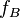 unspecified (note
unspecified (note  ). Thus,
). Thus, 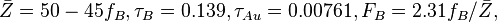 and
and 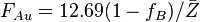 .
.
Damping
Ion acoustic waves are damped both by Coulomb collisions and collisionless Landau damping. The Landau damping occurs on both electrons and ions, with the relative importance depending on parameters.



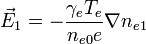
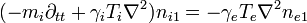
![{\epsilon_0 \over e}\nabla\cdot\vec E = \left[ \sum_{i=1}^N n_{i0}Z_i - n_{ne0} \right] + \left[ \sum_{i=1}^N n_{i1}Z_i - n_{e1} \right]](../I/m/a00cc3766239c9baac3b2b7d12a8e718.png)
![n_{i1} = \gamma_eT_eZ_i {n_{i0} \over n_{e0}} [m_iv_s^2-\gamma_iT_i]^{-1} n_{e1}](../I/m/d46d7f3e955cd60a2f3e9c2f1c4be699.png)
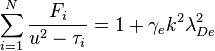

![v_s^2 = {\gamma_eZ_iT_e \over m_i}{1 \over 1+\gamma_e(k\lambda_{De})^2} + {\gamma_iT_{i}\over m_i}
= {\gamma_eZ_iT_e \over m_i} \left[ {1 \over 1+\gamma_e(k\lambda_{De})^2} + {\gamma_iT_{i}\over Z_i\gamma_eT_e} \right]](../I/m/98e4ceb480e3391e439bc3f22a60c898.png)