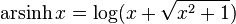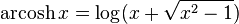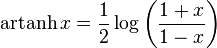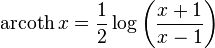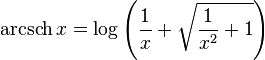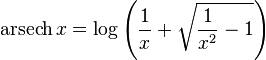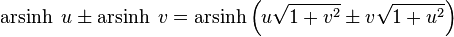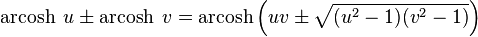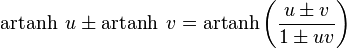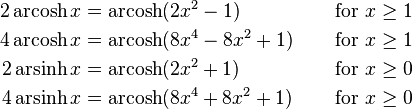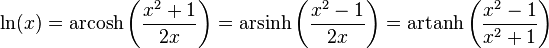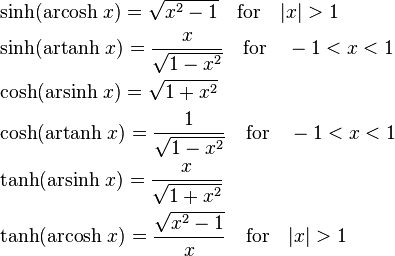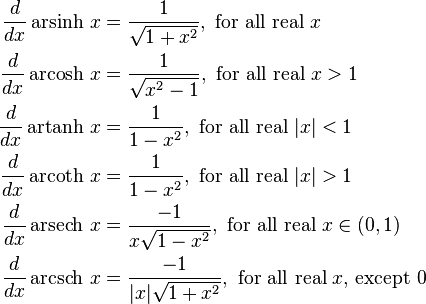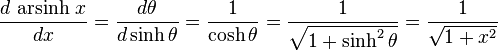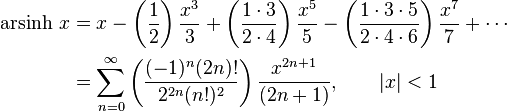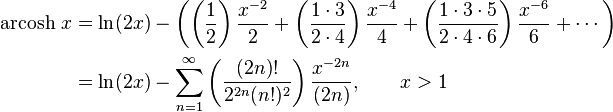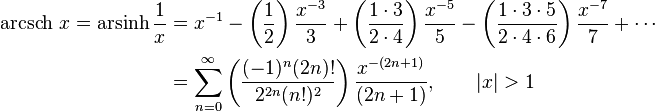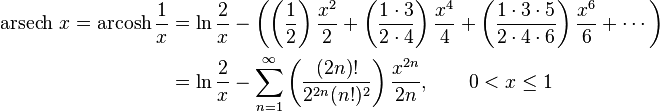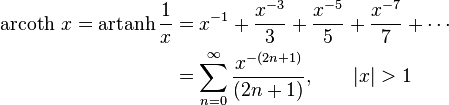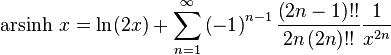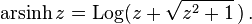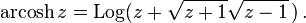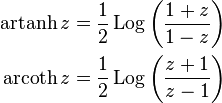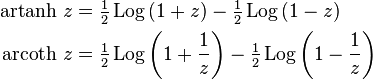Inverse hyperbolic function

The inverse hyperbolic functions.

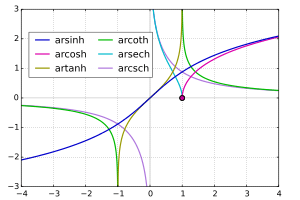
In mathematics, the inverse hyperbolic functions are the inverse functions of the hyperbolic functions.

For a given value of a hyperbolic function, the corresponding inverse hyperbolic function provides a so-called hyperbolic angle. The size of the hyperbolic angle is equal to the area of the corresponding hyperbolic sector of the hyperbola xy = 1, or twice the area of the corresponding sector of the unit hyperbola x² − y² = 1, just as a circular angle is twice the area of the circular sector of the unit circle. Some authors have called inverse hyperbolic functions "area functions" to realize the hyperbolic angles.

Notation

The most common abbreviations are ar- followed by abbreviation of the hyperbolic function (arsinh, arcosh, etc.).

However, arc- followed by the hyperbolic function (for example arcsinh, arccosh), are also commonly seen by analogy with the nomenclature for inverse trigonometric functions. The latter are misnomers, since the prefix arc is the abbreviation for arcus, while the prefix ar stands for area.^[1]^[2]^[3]

Other authors prefer to use the notation argsinh, argcosh, argtanh, and so on, where the prefix arg is the abbreviation of the Latin argumentum.^[4] In computer science this is often shortened to asinh.

The notation sinh⁻¹(x), cosh⁻¹(x), etc., is also used,^[5] despite the fact that care must be taken to avoid misinterpretations of the superscript −1 as a power as opposed to a shorthand for inverse (e.g., cosh⁻¹(x) versus cosh(x)⁻¹).

Definitions in terms of logarithms

As the hyperbolic functions are rational functions of $e x$ whose numerator and denominator are of degree at most two, these functions may be solved in terms of $e x$ , by using the quadratic formula; then, taking the natural logarithm gives the following expressions for the inverse hyperbolic functions.

For complex arguments, the inverse hyperbolic functions, the square root and the logarithm are multi-valued functions, and the equalities of the next subsections may be viewed as equalities of multi-valued functions.

For all inverse hyperbolic functions but the inverse hyperbolic cotangent and the inverse hyperbolic cosecant, the domain of the real function is connected.

Inverse hyperbolic sine

\operatorname{arsinh} x =\log(x + \sqrt{x^2 + 1} )

The domain is the whole real line.

Inverse hyperbolic cosine

\operatorname{arcosh} x =\log(x + \sqrt{x^2-1} )

The domain is the closed interval $[1, +\infty)$ .

Inverse hyperbolic tangent

\operatorname{artanh} x =\frac12\log\left(\frac{1+x}{1-x}\right)

The domain is the open interval $(-1, 1)$ .

Inverse hyperbolic cotangent

\operatorname{arcoth} x = \frac12\log\left(\frac{x+1}{x-1}\right)

The domain is the union of the open intervals $(-\infty, -1)$ and $(1, +\infty)$ .

Inverse hyperbolic cosecant

\operatorname{arcsch} x =\log \left( \frac{1}{x} + \sqrt{\frac{1}{x^2}+ 1} \right)

The domain is the real line with 0 removed.

inverse hyperbolic secant

\operatorname{arsech} x =\log \left( \frac{1}{x}+\sqrt{\frac{1}{x^2}- 1} \right)

The domain is the semi-open interval $(0, 1]$ .

Addition formulae

\operatorname{arsinh} \;u \pm \operatorname{arsinh} \;v = \operatorname{arsinh} \left(u \sqrt{1 + v^2} \pm v \sqrt{1 + u^2}\right)

\operatorname{arcosh} \;u \pm \operatorname{arcosh} \;v = \operatorname{arcosh} \left(u v \pm \sqrt{(u^2 - 1) (v^2 - 1)}\right)

\operatorname{artanh} \;u \pm \operatorname{artanh} \;v = \operatorname{artanh} \left( \frac{u \pm v}{1 \pm uv} \right)

\begin{align}\operatorname{arsinh} \;u + \operatorname{arcosh} \;v & = \operatorname{arsinh} \left(u v + \sqrt{(1 + u^2) (v^2 - 1)}\right) \\ & = \operatorname{arcosh} \left(v \sqrt{1 + u^2} + u \sqrt{v^2 - 1}\right) \end{align}

Other identities

\begin{align} 2\operatorname{arcosh}x&=\operatorname{arcosh}(2x^2-1) &\quad \hbox{ for }x\geq 1 \\ 4\operatorname{arcosh}x&=\operatorname{arcosh}(8x^4-8x^2+1) &\quad \hbox{ for }x\geq 1 \\ 2\operatorname{arsinh}x&=\operatorname{arcosh}(2x^2+1) &\quad \hbox{ for }x\geq 0 \\ 4\operatorname{arsinh}x&=\operatorname{arcosh}(8x^4+8x^2+1) &\quad \hbox{ for }x\geq 0 \end{align}

\ln(x) = \operatorname{arcosh} \left( \frac{x^2 + 1}{2x}\right) = \operatorname{arsinh} \left( \frac{x^2 - 1}{2x}\right) = \operatorname{artanh} \left( \frac{x^2 - 1}{x^2 + 1}\right)

Composition of hyperbolic and inverse hyperbolic functions

\begin{align} &\sinh(\operatorname{arcosh}\,x) = \sqrt{x^{2} - 1} \quad \text{for} \quad |x| > 1 \\ &\sinh(\operatorname{artanh}\,x) = \frac{x}{\sqrt{1-x^{2}}} \quad \text{for} \quad -1 < x < 1 \\ &\cosh(\operatorname{arsinh}\,x) = \sqrt{1+x^{2}} \\ &\cosh(\operatorname{artanh}\,x) = \frac{1}{\sqrt{1-x^{2}}} \quad \text{for} \quad -1 < x < 1 \\ &\tanh(\operatorname{arsinh}\,x) = \frac{x}{\sqrt{1+x^{2}}} \\ &\tanh(\operatorname{arcosh}\,x) = \frac{\sqrt{x^{2} - 1}}{x} \quad \text{for} \quad |x| > 1 \end{align}

Derivatives

\begin{align} \frac{d}{dx} \operatorname{arsinh}\, x & {}= \frac{1}{\sqrt{1+x^2}}, \text{ for all real } x\\ \frac{d}{dx} \operatorname{arcosh}\, x & {}= \frac{1}{\sqrt{x^2-1}}, \text{ for all real } x>1\\ \frac{d}{dx} \operatorname{artanh}\, x & {}= \frac{1}{1-x^2}, \text{ for all real } |x|<1\\ \frac{d}{dx} \operatorname{arcoth}\, x & {}= \frac{1}{1-x^2}, \text{ for all real } |x|>1\\ \frac{d}{dx} \operatorname{arsech}\, x & {}= \frac{-1}{x\sqrt{1-x^2}}, \text{ for all real } x \in (0,1)\\ \frac{d}{dx} \operatorname{arcsch}\, x & {}= \frac{-1}{|x|\sqrt{1+x^2}}, \text{ for all real } x\text{, except } 0\\ \end{align}

For an example differentiation: let θ = arsinh x, so (where sinh² θ = (sinh θ)²):

\frac{d\,\operatorname{arsinh}\, x}{dx} = \frac{d \theta}{d \sinh \theta} = \frac{1} {\cosh \theta} = \frac{1} {\sqrt{1+\sinh^2 \theta}} = \frac{1}{\sqrt{1+x^2}}

Series expansions

Expansion series can be obtained for the above functions:

\begin{align}\operatorname{arsinh}\, x & = x - \left( \frac {1} {2} \right) \frac {x^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^5} {5} - \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^7} {7} +\cdots \\ & = \sum_{n=0}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{2n+1}} {(2n+1)} , \qquad \left| x \right| < 1 \end{align}

\begin{align}\operatorname{arcosh}\, x & = \ln(2x) - \left( \left( \frac {1} {2} \right) \frac {x^{-2}} {2} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{-4}} {4} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{-6}} {6} +\cdots \right) \\ & = \ln(2x) - \sum_{n=1}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{-2n}} {(2n)} , \qquad x > 1 \end{align}

\begin{align}\operatorname{artanh}\, x & = x + \frac {x^3} {3} + \frac {x^5} {5} + \frac {x^7} {7} +\cdots \\ & = \sum_{n=0}^\infty \frac {x^{2n+1}} {(2n+1)} , \qquad \left| x \right| < 1 \end{align}

\begin{align}\operatorname{arcsch}\, x = \operatorname{arsinh} \frac1x & = x^{-1} - \left( \frac {1} {2} \right) \frac {x^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{-5}} {5} - \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{-7}} {7} +\cdots \\ & = \sum_{n=0}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{-(2n+1)}} {(2n+1)} , \qquad \left| x \right| > 1 \end{align}

\begin{align}\operatorname{arsech}\, x = \operatorname{arcosh} \frac1x & = \ln \frac{2}{x} - \left( \left( \frac {1} {2} \right) \frac {x^{2}} {2} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{4}} {4} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{6}} {6} +\cdots \right) \\ & = \ln \frac{2}{x} - \sum_{n=1}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{2n}} {2n} , \qquad 0 < x \le 1 \end{align}

\begin{align}\operatorname{arcoth}\, x = \operatorname{artanh} \frac1x & = x^{-1} + \frac {x^{-3}} {3} + \frac {x^{-5}} {5} + \frac {x^{-7}} {7} +\cdots \\ & = \sum_{n=0}^\infty \frac {x^{-(2n+1)}} {(2n+1)} , \qquad \left| x \right| > 1 \end{align}

Asymptotic expansion for the arsinh x is given by

\operatorname{arsinh}\, x = \ln(2x) + \sum\limits_{n = 1}^\infty {\left( { - 1} \right)^{n - 1} \frac{{\left( {2n - 1} \right)!!}}{{2n\left( {2n} \right)!!}}} \frac{1}{{x^{2n} }}

Principal values in the complex plane

As functions of a complex variable, inverse hyperbolic functions are multivalued functions that are analytics except at a finite number of points. For such a function, it is common to define a principal value, which is a single valued analytic function which coincides with one specific branch of the multivalued function over a domain consisting of the complex plane in which a finite number of arcs (usually half lines or line segments) have been removed. These arcs are called branch cuts. For specifying the branch, that is defining which value of the multivalued function is considered at each point, one generally define it at a particular point, and deduce the value everywhere in the domain of definition of the principal value by analytic continuation. When possible, it is better to define the principal value directly, without referring to analytic continuation.

For example, for the square root, the principal value is defined as the square root that has a positive real part. This defines a single valued analytic function, which is defined everywhere except for non-positive real values of the variables (where the two square roots have a zero real part). This principal value of the square root function is denoted $\sqrt x$ in what follows. 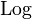Similarly, the principal value of the logarithm, denoted $\operatorname{Log}$ in what follows, is defined as the value for which the imaginary part as the smallest absolute value. It is defined everywhere except for non positive real values of the variable, for which two different values of the logarithm reach the minimum.

For all inverse hyperbolic functions, the principal value may be defined in terms of principal values of the square root and the logarithm function. However, in some cases, the formulas of § Definitions in terms of logarithms do not give a correct principal value, as giving a domain of definition which is too small and, in one case non-connected.

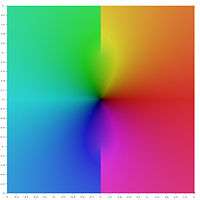
Principal value of the inverse hyperbolic sine

The principal value of the inverse hyperbolic sine is given by

\operatorname{arsinh} z = \operatorname{Log}(z + \sqrt{z^2 + 1} \,)\,.

The argument of the square root is a non-positive real number if and only if $z$ belongs to one of the intervals $[i, + i \infty)$ and $(- i \infty, - i]$ of the imaginary axis. If the argument of the logarithm is real, then it is positive. Thus this formula defines a principal value for arsinh with branch cuts $[i, + i \infty)$ and $(- i \infty, - i]$ . This is optimal, as the branch cuts must connect the singular points $i$ and $- i$ to the infinity.

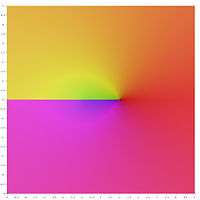
Principal value of the inverse hyperbolic cosine

The formula for the inverse hyperbolic cosine given in § Inverse hyperbolic cosine is not convenient, as, with principal values of the logarithm and the square root, the principal value of arcsinh would not been defined for imaginary $z$ . Thus the square root has to be factorized, leading to

\operatorname{arcosh} z = \operatorname{Log}(z + \sqrt{z+1} \sqrt{z-1} \,)\,.

The principal values of the square roots are both defined except if $z$ belongs to the real interval $(-\infty, 1]$ . If the argument of the logarithm is real, then $z$ is real and has the same sign. Thus, the above formula defines a principal value of arcosh outside the real interval $(-\infty, 1]$ , which is thus the unique branch cut.

Principal values of the inverse hyperbolic tangent and cotangent

The formulas given in § Definitions in terms of logarithms suggests

\begin{align} \operatorname{artanh} z &=\frac12\operatorname{Log}\left(\frac{1+z}{1-z}\right) \\ \operatorname{arcoth} z &= \frac12\operatorname{Log}\left(\frac{z+1}{z-1}\right) \end{align}

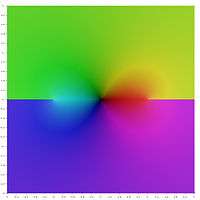
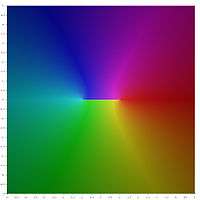
for the definition of the principal values of inverse hyperbolic tangent and cotangent. In these formulas, the argument of the logarithm is real if and only if $z$ is real. For artanh, this argument is in the real interval $(-\infty, 0]$ if $z$ belongs either to $(-\infty, -1]$ or to $[1, \infty)$ . For arcoth, the argument of the logarithm is in $(-\infty, 0]$ if and only if $z$ belongs to the real interval $[-1, 1]$ .

Therefore, these formulas define convenient principal values, for which the branch cuts are $(-\infty, -1]$ and $[1, \infty)$ for the inverse hyperbolic tangent, and $[-1, 1]$ for the inverse hyperbolic cotangent.

In view of a better numerical evaluation near the branch cuts, some author use the following equivalent definition of the principal values, although the second one introduces an removable singularity at $z = 0$ .

\begin{align} \operatorname{artanh}\, z &= \tfrac12\operatorname{Log}\left({1+z}\right) - \tfrac12\operatorname{Log}\left({1-z}\right) \\ \operatorname{arcoth}\, z &= \tfrac12\operatorname{Log}\left({1+\frac{1}{z} }\right) - \tfrac12\operatorname{Log}\left({1-\frac{1}{z}}\right) \end{align}

Principal value of the inverse hyperbolic cosecant

For inverse hyperbolic cosecant, the principal value is defined as

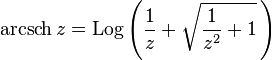\operatorname{arcsch} z = \operatorname{Log}\left( \frac{1}{z} + \sqrt{ \frac{1}{z^2} +1 } \,\right)

It is defined when the arguments of the logarithm and the square root are not non-positive real numbers. The principal value of the square root is thus defined outside the interval $[- i, i]$ of the imaginary line. If the argument of the logarithm is real, then $z$ is a non-zero real number, and this implies that the argument of the logarithm is positive.

Thus the principal value is defined by the above formula outside the branch cut consisting of the interval $[- i, i]$ of the imaginary line.

For $z = 0$ , there is a singular point that is included in the branch cut.

Principal value of the inverse hyperbolic secant

Here, as in the case of the inverse hyperbolic cosine, we have to factorize the square root. This gives the principal value

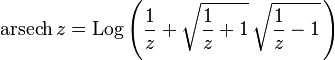\operatorname{arsech} z = \operatorname{Log}\left( \frac{1}{z} + \sqrt{ \frac{1}{z} + 1 } \, \sqrt{ \frac{1}{z} -1 } \,\right)

If the argument of a square root is real, then $z$ is real, and it follows that both principal values of square roots are defined except if $z$ is real and belongs to one of the intervals $(-\infty, 0]$ and $[1, +\infty)$ . If the argument of the logarithm is real and negative, then $z$ is also real and negative. It follows that the principal value of arsech is well defined by the above formula outside two branch cuts, the real intervals $(-\infty, 0]$ and $[1, +\infty)$ .

For $z = 0$ , there is a singular point that is included in one of the branch cuts.

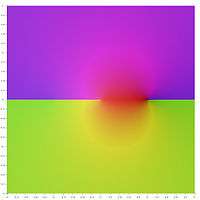
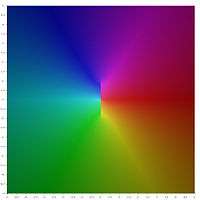
Graphical representation

In the following graphical representation of the principal values of the inverse hyperbolic functions, the branch cuts appear as discontinuities of the color. The fact that the whole branch cuts appear as discontinuities, shows that these principal values may not be extended into analytic functions defined over larger domains. In other words, the above defined branch cuts are minimal.

Square representing central portion of the complex z-plane painted in psychedelic colours

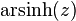
\operatorname{arsinh}(z)

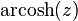
\operatorname{arcosh}(z)

\operatorname{artanh}(z)

\operatorname{arcoth}(z)

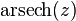
\operatorname{arsech}(z)

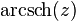
\operatorname{arcsch}(z)

Inverse hyperbolic functions in the complex z-plane: the colour at each point in the plane represents the complex value of the respective function at that point

References

↑ As stated by Jan Gullberg, Mathematics: From the Birth of Numbers (New York: W. W. Norton & Company, 1997), ISBN 0-393-04002-X, p. 539:
Another form of notation, arcsinh x, arccosh x, etc., is a practice to be condemned as these functions have nothing whatever to do with arc, but with area, as is demonstrated by their full Latin names,
arsinh area sinus hyperbolicus
arcosh area cosinus hyperbolicus, etc.
↑ As stated by Eberhard Zeidler, Wolfgang Hackbusch and Hans Rudolf Schwarz, translated by Bruce Hunt, Oxford Users' Guide to Mathematics (Oxford: Oxford University Press, 2004), ISBN 0-19-850763-1, Section 0.2.13: "The inverse hyperbolic functions", p. 68: "The Latin names for the inverse hyperbolic functions are area sinus hyperbolicus, area cosinus hyperbolicus, area tangens hyperbolicus and area cotangens hyperbolicus (of x). ..." This aforesaid reference uses the notations arsinh, arcosh, artanh, and arcoth for the respective inverse hyperbolic functions.
↑ As stated by Ilja N. Bronshtein, Konstantin A. Semendyayev, Gerhard Musiol and Heiner Muehlig, Handbook of Mathematics (Berlin: Springer-Verlag, 5th ed., 2007), ISBN 3-540-72121-5, doi:10.1007/978-3-540-72122-2, Section 2.10: "Area Functions", p. 91:
The area functions are the inverse functions of the hyperbolic functions, i.e., the inverse hyperbolic functions. The functions sinh x, tanh x, and coth x are strictly monotone, so they have unique inverses without any restriction; the function cosh x has two monotonic intervals so we can consider two inverse functions. The name area refers to the fact that the geometric definition of the functions is the area of certain hyperbolic sectors ...
↑ Bacon, Harold Maile (1942). Differential and Integral Calculus. McGraw-Hill. p. 203.
↑ Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (1992). "Section 5.6. Quadratic and Cubic Equations". Numerical Recipes in FORTRAN: The Art of Scientific Computing (2nd ed.). New York: Cambridge University Press. ISBN 0-521-43064-X.

Herbert Busemann and Paul J. Kelly (1953) Projective Geometry and Projective Metrics, page 207, Academic Press.

External links

Hazewinkel, Michiel, ed. (2001), "Inverse hyperbolic functions", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Inverse hyperbolic functions at MathWorld

This article is issued from Wikipedia - version of the Friday, February 12, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.