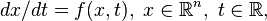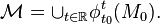Invariant manifold
In dynamical systems, a branch of mathematics, an invariant manifold is a topological manifold that is invariant under the action of the dynamical system.[1] Examples include the slow manifold, center manifold, stable manifold, unstable manifold, subcenter manifold and inertial manifold.
Typically, although by no means always, invariant manifolds are constructed as a 'perturbation' of an invariant subspace about an equilibrium. In dissipative systems, an invariant manifold based upon the gravest, longest lasting modes forms an effective low-dimensional, reduced, model of the dynamics. [2]
Definition
Consider the differential equation 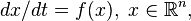 with flow
with flow  being the solution of the differential equation with
being the solution of the differential equation with 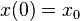 .
A set
.
A set 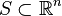 is called an invariant set for the differential equation if, for each
is called an invariant set for the differential equation if, for each 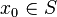 , the solution
, the solution 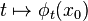 , defined on its maximal interval of existence, has its image in
, defined on its maximal interval of existence, has its image in  . Alternatively, the orbit
passing through each
. Alternatively, the orbit
passing through each 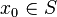 lies in
lies in  . In addition,
. In addition,  is called an invariant manifold if
is called an invariant manifold if  is a manifold.
[3]
is a manifold.
[3]
Examples
Simple 2D dynamical system
For any fixed parameter  , consider the variables
, consider the variables 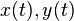 governed by the pair of coupled differential equations
governed by the pair of coupled differential equations
The origin is an equilibrium. This system has two invariant manifolds of interest through the origin.
- The vertical line
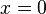 is invariant as when
is invariant as when 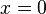 the
the  -equation becomes
-equation becomes 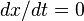 which ensures
which ensures  remains zero. This invariant manifold,
remains zero. This invariant manifold, 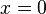 , is a stable manifold of the origin (when
, is a stable manifold of the origin (when 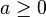 ) as all initial conditions
) as all initial conditions 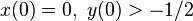 lead to solutions asymptotically approaching the origin.
lead to solutions asymptotically approaching the origin. - The parabola
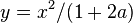 is invariant for all parameter
is invariant for all parameter  . One can see this invariance by considering the time derivative
. One can see this invariance by considering the time derivative ![d/dt[y-x^2/(1+2a)]](../I/m/7d6b53129d8294d4c159ae1d31daa8da.png) and finding it is zero on
and finding it is zero on 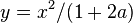 as required for an invariant manifold. For
as required for an invariant manifold. For  this parabola is the unstable manifold of the origin. For
this parabola is the unstable manifold of the origin. For  this parabola is a center manifold, more precisely a slow manifold, of the origin.
this parabola is a center manifold, more precisely a slow manifold, of the origin. - For
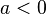 there is only an invariant stable manifold about the origin, the stable manifold including all
there is only an invariant stable manifold about the origin, the stable manifold including all 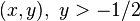 .
.
Invariant manifolds in non-autonomous dynamical systems
A differential equation
represents a non-autonomous dynamical system, whose solutions are of the form 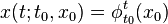 with
with 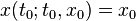 . In the extended phase space
. In the extended phase space 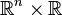 of such a system, any initial surface
of such a system, any initial surface 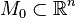 generates an invariant manifold
generates an invariant manifold
A fundamental question is then how one can locate, out of this large family of invariant manifolds, the ones that have the highest influence on the overall system dynamics. These most influential invariant manifolds in the extended phase space of a non-autonomous dynamical systems are known as Lagrangian Coherent Structures.[4]
See also
References
- ↑ Hirsh M.W., Pugh C.C., Shub M., Invariant Manifolds, Lect. Notes. Math., 583, Springer, Berlin — Heidelberg, 1977
- ↑ A. J. Roberts. The utility of an invariant manifold description of the evolution of a dynamical system. SIAM J. Math. Anal., 20:1447–1458, 1989. http://locus.siam.org/SIMA/volume-20/art_0520094.html
- ↑ C. Chicone. Ordinary Differential Equations with Applications, volume 34 of Texts in Applied Mathematics. Springer, 2006, p.34
- ↑ Haller, G. (2015). "Lagrangian Coherent Structures". Annual Review of Fluid Mechanics 47: 137. Bibcode:2015AnRFM..47..137H. doi:10.1146/annurev-fluid-010313-141322.