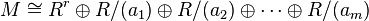Invariant factor

The invariant factors of a module over a principal ideal domain (PID) occur in one form of the structure theorem for finitely generated modules over a principal ideal domain.

If $R$ is a PID and $M$ a finitely generated $R$ -module, then

M\cong R^r\oplus R/(a_1)\oplus R/(a_2)\oplus\cdots\oplus R/(a_m)

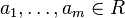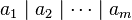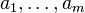for some integer $r\geq0$ and a (possibly empty) list of nonzero elements $a_1,\ldots,a_m\in R$ for which $a_1 \mid a_2 \mid \cdots \mid a_m$ . The nonnegative integer $r$ is called the free rank or Betti number of the module $M$ , while $a_1,\ldots,a_m$ are the invariant factors of $M$ and are unique up to associatedness.

The invariant factors of a matrix over a PID occur in the Smith normal form and provide a means of computing the structure of a module from a set of generators and relations.

References

B. Hartley; T.O. Hawkes (1970). Rings, modules and linear algebra. Chapman and Hall. ISBN 0-412-09810-5. Chap.8, p.128.
Chapter III.7, p.153 of Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0, Zbl 0848.13001

This article is issued from Wikipedia - version of the Monday, May 12, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Invariant factor

See also

References