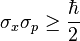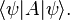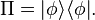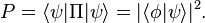Interpretations of quantum mechanics

Quantum mechanics
Uncertainty principle
Introduction Glossary History
Background Classical mechanics Old quantum theory Bra–ket notation Hamiltonian Interference
Fundamentals Complementarity Decoherence Entanglement Energy level Measurement Nonlocality Quantum number State Superposition Symmetry Tunnelling Uncertainty Wave function (collapse)
Experiments Afshar Bell's inequality Davisson–Germer Double-slit Elitzur–Vaidman Franck–Hertz Mach–Zehnder Popper Quantum eraser (delayed-choice) Schrödinger's cat Stern–Gerlach Wheeler's delayed-choice
Formulations Overview Heisenberg Interaction Matrix Phase-space Schrödinger Sum-over-histories (path integral)
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Overview Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Many-worlds Objective collapse Bayesian Quantum logic Relational Stochastic Scale relativity Transactional
Advanced topics Quantum chaos Quantum computing Density matrix Quantum field theory Fractional quantum mechanics Quantum information science Relativistic quantum mechanics Scattering theory Quantum statistical mechanics
Scientists Aharonov Bell Blackett Bloch Bohm Bohr Born Bose de Broglie Candlin Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Pauli Lamb Landau Laue Moseley Millikan Onnes Planck Rabi Raman Rydberg Schrödinger Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger

Interpretations of quantum mechanics deal with two problems: how to relate the mathematical formalism of quantum mechanics to empirical observations; and how to understand that relation in physical and metaphysical terms and in ordinary language. The mathematico-empirical relation, though needing experience for its understanding, is relatively well agreed upon, and is supported by rigorous and thorough experimental testing. But the physical and metaphysical questions give rise to doubt and contention over what is the place and character of causality in atomic and sub-atomic physics, how far quantum mechanics is limited to what can be known with certainty, what is physical reality, and other questions.

History of interpretations

The definition of quantum theorists' terms, such as wavefunctions and matrix mechanics, progressed through many stages. For instance, Erwin Schrödinger originally viewed the electron's wavefunction as its charge density smeared across the field, whereas Max Born reinterpreted it as the electron's probability density distributed across the field. There was detailed and vigorous debate about this and many other related questions at the fifth Solvay Conference in 1927.^[1] Debate has continued right to present times.^[2][3]

The eponym Copenhagen interpretation is often used; it seems to have been invented by Heisenberg in 1955. Its exact meaning is not agreed upon. It is sometimes said to refer to the orthodox or standard interpretation. One may look cautiously for its meaning in the opinions of Bohr, Heisenberg, Born, and perhaps Dirac, especially those offered before 1928.^[4][5][6][7]

Amongst more recent interpretational concepts are quantum decoherence^{[8][9][10][11]} and many worlds.^[12][13][14]

During most of the 20th century, collapse theories were clearly the mainstream view, and the question of "interpretation" of quantum mechanics mostly revolved around how to interpret "collapse". Proponents of either "pilot-wave" (de Broglie-Bohm-like) or "many-worlds" (Everettian) interpretations tend to emphasize how their respective camps were intellectually marginalized throughout 1950s to 1980s. In this sense, all non-collapse theories are (historically) "minority" interpretations.

However, since the 1990s, there has been a resurgence of interest in non-collapse theories. The Stanford Encyclopedia as of 2015 groups interpretations of quantum mechanics into "Bohmian mechanics" (pilot-wave theories),^[15] "collapse theories",^[16] "many-worlds interpretations",^[17] "modal interpretation"^[18] and "relational interpretations"^[19] as classes of into which most suggestions may be grouped.

As a rough guide development of the mainstream view during the 1990s to 2000s, consider the "snapshot" of opinions collected in a poll by Schlosshauer et al. at the 2011 "Quantum Physics and the Nature of Reality" conference of July 2011.^[20] The authors reference a similarly informal poll carried out by Max Tegmark at the "Fundamental Problems in Quantum Theory" conference in August 1997. The main conclusion of the authors is that "the Copenhagen interpretation still reigns supreme", receiving the most votes in their poll (42%), besides the rise to mainstream notability of the many-worlds interpretations:

"The Copenhagen interpretation still reigns supreme here, especially if we lump it together with intellectual offsprings such as information-based interpretations and the Quantum Bayesian interpretation. In Tegmark's poll, the Everett interpretation received 17% of the vote, which is similar to the number of votes (18%) in our poll."

Nature of interpretation

An interpretation of quantum mechanics is a conceptual or argumentative way of relating between:

• the mathematical formalism of quantum mechanics—mathematical objects, such as wave functions, state vectors, the Schrödinger equation, and
• the experimental facts of quantum physics—how laboratory devices are used to make observations in empirical investigations, and
• the physical meaning of the formalism and the experimental facts, in terms of ordinary understanding, and in more philosophical terms.

Two philosophical, or more precisely, two metaphysical aspects are relevant:

1. Ontology—claims about what things, such as categories and entities, exist in the world, and what theoretical objects are related to those real existents
2. Epistemology—claims about the possibility, scope, and means toward relevant knowledge of the world

In philosophy of science, the distinction of knowledge versus reality is termed epistemic versus ontic. A general law is a regularity of outcomes (epistemic), whereas a causal mechanism may regulate the outcomes (ontic). A phenomenon can receive interpretation either ontic or epistemic. For instance, indeterminism may be attributed to limitations of human observation and perception (epistemic), or may be explained as a real existing maybe encoded in the universe (ontic). Confusing the epistemic with the ontic, like if one were to presume that a general law actually "governs" outcomes—and that the statement of a regularity has the role of a causal mechanism—is a category mistake.

In a broad sense, scientific theory can be viewed as offering scientific realism—approximately true description or explanation of the natural world—or might be perceived with antirealism. A realist stance seeks the epistemic and the ontic, whereas an antirealist stance seeks epistemic but not the ontic. In the 20th century's first half, antirealism was mainly logical positivism, which sought to exclude unobservable aspects of reality from scientific theory.

Since the 1950s, antirealism is more modest, usually instrumentalism, permitting talk of unobservable aspects, but ultimately discarding the very question of realism and posing scientific theory as a tool to help humans make predictions, not to attain metaphysical understanding of the world. The instrumentalist view is carried by the famous quote of David Mermin, "Shut up and calculate".^[21]

Opinions vary: J.S. Bell was interested in debate along Bohr–Einstein lines, but recognized that important contributors to quantum mechanics were not. He wrote of "why bother?'ers", for example Paul Dirac.^[22] Although Dirac wrote significantly on the physical aspects of orthodox interpretation,^[23] he wrote about the debate: "I was not very much interested. I was more interested in getting the correct equations."^[24] Dirac's final written words on the subject were: "The interpretation of quantum mechanics has been dealt with by many authors, and I do not want to discuss it here. I want to deal with more fundamental things."^[25] Other physicists that might be included in the "why bother?'ers" category are John Ward, Nico van Kampen, Willis Lamb, Richard Dalitz, and even Richard Feynman.

However, some philosophers appear to have a different opinion to that of Bell on the leanings of Dirac.^[26]

Other approaches to resolve conceptual problems introduce new mathematical formalism, and so propose additional theories with their interpretations. An example is Bohmian mechanics, which is empirically equivalent with the standard formalisms, but requires extra equations to describe the precise trajectories that it postulates.

Challenges for interpretations

Interpretations of quantum mechanics attempt to provide a conceptual framework for understanding the many aspects of quantum mechanics which are not easily handled by the conceptual framework used for classical physics:

1. Abstract, mathematical nature of quantum field theories
2. Existence of apparently indeterministic and yet reversible processes
3. Role of the observer in determining outcomes
4. Distinction between preparation and measurement
5. Correlations between remote objects
6. Complementarity of offered descriptions
7. Rapidly rising intricacy, far exceeding humans' present calculational capacity, as a system's size increases

The mathematical structure of quantum mechanics is based on rather abstract mathematics, like Hilbert spaces. In classical field theory, a physical property at a given location in the field is readily derived. In Heisenberg's formalism, on the other hand, to derive physical information about a location in the field, one must apply a quantum operation to a quantum state, an elaborate mathematical process.^[27]

Schrödinger's formalism describes a waveform governing the probability of outcomes across a field. Yet how do we find in a specific location a particle whose wavefunction, a mere probability distribution of existence, spans a vast region of space?

The act of measurement can interact with the system state in peculiar ways, as found in double-slit experiments. The Copenhagen interpretation holds that the myriad probabilities across a quantum field are unreal, yet that the act of observation/measurement collapses the wavefunction and sets a single possibility to become real. Yet quantum decoherence grants that all the possibilities can be real, and that the act of observation/measurement sets up new subsystems.^[28]

A key interpretational question is posed by Dirac's famous sentences about quantum interference: "Each photon then interferes only with itself. Interference between two different photons never occurs." Dirac stops short of repeating this statement for objects other than photons, such as electrons, contenting himself with saying "... for particles even as light as electrons the associated wave frequency is so high that it is not easy to demonstrate interference."^[29] Dirac was of course well familiar with the concept of electron diffraction by crystals, which is usually regarded as an interference phenomenon. The comments of Dirac surrounding these sentences indicate that he considers them to be interpretive. No experiment can directly test them, an actual particular photon being detectable only once.

Quantum entanglement, as illustrated in the EPR paradox, seemingly violates principles of local causality.^[30]

Complementarity holds that no set of classical physical concepts can simultaneously refer to all properties of a quantum system. For instance, wave description A and particulate description B can each describe a quantum system S, but not simultaneously. Still, complementarity does not usually imply that classical logic is at fault (although Hilary Putnam took such view in "Is logic empirical?"); rather, the composition of physical properties of S does not obey the rules of classical propositional logic when using propositional connectives (see "Quantum logic"). As now well known, the "origin of complementarity lies in the non-commutativity of operators" that describe quantum objects (Omnès 1999).

Instrumentalist description

Any modern scientific theory requires at the very least a description that relates the mathematical formalism to experimental practice and prediction. In the case of quantum mechanics, the most common description is an assertion of statistical regularity between state preparation processes and measurement processes. That is, if a measurement of a real-value quantity is performed many times, each time starting with the same initial conditions, the outcome is a well-defined probability distribution agreeing with the real numbers; moreover, quantum mechanics provides a computational instrument to determine statistical properties of this distribution, such as its expectation value.

Calculations for measurements performed on a system S postulate a Hilbert space H over the complex numbers. When the system S is prepared in a pure state, it is associated with a vector in H. Measurable quantities are associated with Hermitian operators acting on H: these are referred to as observables.

Repeated measurement of an observable A where S is prepared in state ψ yields a distribution of values. The expectation value of this distribution is given by the expression

This mathematical machinery gives a simple, direct way to compute a statistical property of the outcome of an experiment, once it is understood how to associate the initial state with a Hilbert space vector, and the measured quantity with an observable (that is, a specific Hermitian operator).^[31]

As an example of such a computation, the probability of finding the system in a given state 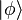is given by computing the expectation value of a (rank-1) projection operator.

The probability is then the non-negative real number given by

In the context of quantum mechanics, the "instrumentalist interpretation" refers to the position that there can be no meaningful "interpretation" beyond the mere instrumentalist description, a position often equated with eschewing all interpretation. It is summarized by the sentence "Shut up and calculate!".^{[32] [33]} Depending on the understanding of the term instrumentalism, the "instrumentalist" or "shut up and calculate"-interpretation may either express pragmatism (the formalism of quantum mechanics has no application outside of the description of predicting experimental outcomes) or radical empiricism or phenomenalism (there is no valid concept of reality outside of perceptual phenomena).

Concerns of Einstein

An interpretation of the mathematical formalism of quantum mechanics can be characterized by its treatment of some physical or micro-cosmological problems that Einstein saw in Copenhagenism, such as:

• Realism
• Completeness
• Local realism
• Determinism
• Causality

To explain these problems, we need to be more explicit about the kind of picture an interpretation provides. To that end we will regard an interpretation as a correspondence between the elements of the mathematical formalism M and the elements of an interpreting structure I, where:

• The mathematical formalism M consists of the Hilbert space machinery of ket-vectors, self-adjoint operators acting on the space of ket-vectors, unitary time dependence of the ket-vectors, and measurement operations. In this context a measurement operation is a transformation which turns a ket-vector into a probability distribution (for a formalization of this concept see quantum operations).
• The interpreting structure I includes states, transitions between states, measurement operations, and possibly information about spatial extension of these elements. A measurement operation refers to an operation which returns a value and might result in a system state change. Spatial information would be exhibited by states represented as functions on configuration space. The transitions may be non-deterministic or probabilistic or there may be infinitely many states.

One way of assessing an interpretation is whether the elements of I are regarded as physically real. Hence the bare instrumentalist view of quantum mechanics outlined in the previous section is not an interpretation at all, for it makes no claims about elements of physical reality.

The current usage of realism and completeness originated in the 1935 paper in which Einstein and others proposed the EPR paradox.^[34] In that paper the authors proposed the concepts of element of reality and of completeness of a physical theory. They characterised element of reality as a quantity whose value can be predicted with certainty before measuring or otherwise disturbing it, and defined a complete physical theory as one in which every element of physical reality is accounted for by the theory. The paper proposed that an interpretation is complete if every element of the interpreting structure is present in the mathematics. Realism is also a property of each of the elements of the maths; an element is real if it corresponds to something physical in the interpreting structure. For example, in some interpretations of quantum mechanics (such as the many-worlds interpretation) the ket vector associated to the system state is said to correspond to an element of physical reality, while in other interpretations it is not. Einstein was not the active author of the EPR paper, and it did not quite focus on his principal concern, which was about causality.

Determinism is a property characterizing state changes due to the passage of time, namely that the state at a future instant is a uniquely defined mathematical function of the state in the present (see time evolution). It may not always be clear whether a particular interpretation is deterministic or not, as there may not be a clear choice of a time parameter. Moreover, a given theory may have two interpretations, one of which is deterministic and the other not.

Local realism is an attempt to formulate in relevant mathematical terms the subtle physical, micro-cosmological, or metaphysical concept of causality. It has two aspects:

• The value returned by a measurement corresponds to the value of some function in the state space. In other words, that value is an element of reality;
• The effects of measurement have a propagation speed not exceeding some universal limit (e.g. the speed of light). In order for this to make sense, measurement operations in the interpreting structure must be localized.

A formulation of local realism in terms of a local hidden variable theory was proposed by John Bell. This is expressed in what is widely called Bell's theorem. This, combined with experimental testing, is regarded by some physicists as restricting the kinds of properties that a quantum theory can have, the primary proposed implication being that quantum mechanics cannot satisfy both the principle of locality and counterfactual definiteness.

Summary of interpretations

Collapse theories

The Copenhagen interpretation

The Copenhagen interpretation is the interpretation of quantum mechanics formulated by Niels Bohr and Werner Heisenberg while collaborating in Copenhagen around 1927. For most of the twentieth century it was regarded as the "standard" interpretation. Bohr and Heisenberg extended the probabilistic interpretation of the wavefunction proposed originally by Max Born. The Copenhagen interpretation rejects questions like "where was the particle before I measured its position?" as meaningless. The measurement process picks out exactly one of the many possibilities allowed for by the state's wave function in a manner consistent with the well-defined probabilities that are assigned to each possible state. According to the interpretation, the interaction of an observer or apparatus that is external to the quantum system is the cause of wave function collapse, thus according to Paul Davies, "reality is in the observations, not in the electron".^[35]

Consciousness causes collapse

In his treatise The Mathematical Foundations of Quantum Mechanics, John von Neumann deeply analyzed the so-called measurement problem. He concluded that the entire physical universe could be made subject to the Schrödinger equation (the universal wave function). He also described how measurement could cause a collapse of the wave function.^[36] This point of view was prominently expanded on by Eugene Wigner, who argued that human experimenter consciousness (or maybe even dog consciousness) was critical for the collapse, but he later abandoned this interpretation.^[37][38]

Variations of the von Neumann interpretation include:

Subjective reduction research

This principle, that consciousness causes the collapse, is the point of intersection between quantum mechanics and the mind/body problem; and researchers are working to detect conscious events correlated with physical events that, according to quantum theory, should involve a wave function collapse; but, thus far, results are inconclusive.^[39][40][41]

Participatory anthropic principle (PAP)

Main article: Anthropic principle

John Archibald Wheeler's participatory anthropic principle says that consciousness plays some role in bringing the universe into existence.^[42]

Other physicists have elaborated their own variations of the von Neumann interpretation; including:

• Henry P. Stapp (Mindful Universe: Quantum Mechanics and the Participating Observer)
• Bruce Rosenblum and Fred Kuttner (Quantum Enigma: Physics Encounters Consciousness)

Objective collapse theories

Objective collapse theories differ from the Copenhagen interpretation in regarding both the wavefunction and the process of collapse as ontologically objective. In objective theories, collapse occurs randomly ("spontaneous localization"), or when some physical threshold is reached, with observers having no special role. Thus, they are realistic, indeterministic, no-hidden-variables theories. The mechanism of collapse is not specified by standard quantum mechanics, which needs to be extended if this approach is correct, meaning that Objective Collapse is more of a theory than an interpretation. Examples include the Ghirardi-Rimini-Weber theory^[43] and the Penrose interpretation.^[44]

Many worlds theories

The many-worlds interpretation is an interpretation of quantum mechanics in which a universal wavefunction obeys the same deterministic, reversible laws at all times; in particular there is no (indeterministic and irreversible) wavefunction collapse associated with measurement. The phenomena associated with measurement are claimed to be explained by decoherence, which occurs when states interact with the environment producing entanglement, repeatedly splitting the universe into mutually unobservable alternate histories—distinct universes within a greater multiverse. In this interpretation the wavefunction has objective reality.

Many minds

The many-minds interpretation of quantum mechanics extends the many-worlds interpretation by proposing that the distinction between worlds should be made at the level of the mind of an individual observer.

Hidden variables

Pilot-wave theories

The de Broglie–Bohm or "pilot wave" theories form a class of interpretations of quantum mechanics based on a theory of Louis de Broglie later extended by David Bohm. Particles, which always have positions, are guided by the wavefunction. The wavefunction evolves according to the Schrödinger wave equation, and the wavefunction never collapses. The theory takes place in a single space-time, is non-local, and is deterministic. The simultaneous determination of a particle's position and velocity is subject to the usual uncertainty principle constraint. The theory is considered to be a hidden variable theory, and by embracing non-locality it satisfies Bell's inequality. The measurement problem is resolved, since the particles have definite positions at all times.^[45] The appearance of collapse is explained as phenomenological.^[46]

Time-symmetric theories

Several theories have been proposed which modify the equations of quantum mechanics to be symmetric with respect to time reversal.^{[47][48][49][50][51][52]} (E.g. see Wheeler–Feynman time-symmetric theory). This creates retrocausality: events in the future can affect ones in the past, exactly as events in the past can affect ones in the future. In these theories, a single measurement cannot fully determine the state of a system (making them a type of hidden variables theory), but given two measurements performed at different times, it is possible to calculate the exact state of the system at all intermediate times. The collapse of the wavefunction is therefore not a physical change to the system, just a change in our knowledge of it due to the second measurement. Similarly, they explain entanglement as not being a true physical state but just an illusion created by ignoring retrocausality. The point where two particles appear to "become entangled" is simply a point where each particle is being influenced by events that occur to the other particle in the future.

Not all advocates of time-symmetric causality favour modifying the unitary dynamics of standard quantum mechanics. Thus a leading exponent of the two-state vector formalism, Lev Vaidman, highlights how well the two-state vector formalism dovetails with Hugh Everett's many-worlds interpretation.^[53]

Transactional Interpretation

The transactional interpretation of quantum mechanics (TIQM) by John G. Cramer is an interpretation of quantum mechanics inspired by the Wheeler–Feynman absorber theory.^[54] It describes a quantum interaction in terms of a standing wave formed by the sum of a retarded (forward-in-time) and an advanced (backward-in-time) wave. The author argues that it avoids the philosophical problems with the Copenhagen interpretation and the role of the observer, and resolves various quantum paradoxes.

Stochastic mechanics

An entirely classical derivation and interpretation of Schrödinger's wave equation by analogy with Brownian motion was suggested by Princeton University professor Edward Nelson in 1966.^[55] Similar considerations had previously been published, for example by R. Fürth (1933), I. Fényes (1952), and Walter Weizel (1953), and are referenced in Nelson's paper. More recent work on the stochastic interpretation has been done by M. Pavon.^[56] An alternative stochastic interpretation was developed by Roumen Tsekov.^[57]

Scale relativity

An approach closely related to stochastic mechanics is scale relativity developed by Laurent Nottale. The main difference with stochastic mechanics is that the stochastic fluctuations which transform classical mechanics into quantum mechanics are the consequence of the scale relativistic nature of the law of motion. This is a generalisation of Einstein's theory of relativity to include scale transformations. It is scale covariance that makes spacetime fractal and hence particle paths become non-differentiable fractal paths just like quantum paths.

Scale relativity is also more general than Nelson stochastic mechanics since it not only derives the Schrödinger equation from quantum mechanics but also the equations of quantum field theory. Depending of the form of the scale covariance law one gets different theories ranging from standard non-relativistic quantum mechanics, over non-linear non-relativistic Schrödinger equations, to relativistic quantum mechanics (Klein-Gordon & Dirac equation) and various quantum field theories.

Popper's experiment

Karl Popper took part in the "EPR controversy", by exchanging letters with Einstein, Bell etc. about the issue, and by proposing his own Bell test experiment. Popper first proposed an experiment that would test indeterminacy in Quantum Mechanics in two works of 1934.^[58][59] However, Einstein wrote a letter to Popper about the experiment in which he raised some crucial objections, causing Popper to admit that his initial idea was "based on a mistake".^[60] In the 1950s he returned to the subject and formulated this later experiment, which was finally published in 1982.^[61][62]

Since Popper holds both counterfactual definiteness and locality to be true, it is under dispute whether his view is an interpretation (which is what he claimed) or a modification of Quantum Mechanics (which is what many Physicists claim), and, in case of the latter, if it has been empirically refuted or not by Bell test experiments.

Other than that, Popper's theory is a variant of the de Broglie–Bohm theory that interprets the probabilities as a stochastic element in the particle movement instead of uncertainties in their initial position. In this sense it is a position between de Broglie–Bohm and stochastic mechanics, accepting the reality of the wave function like the former (in Popper's view, it is a propensity field), and the stochastic element like the latter (see also note 138 in Popper's autobiography Unended Quest, where he expresses some sympathy for Nelson's stochastic interpretation).

Information-based interpretations

Quantum informational approaches have attracted growing support during the 2000s.^[63] Hagar and Hemmo (2008) even refer to it (critically) as "a new orthodoxy in the foundations of quantum mechanics."^[64]

J. A. Wheeler (1990) with his "It from Bit" ("It": physical entity, "Bit": unit of information) has been described as "the cheerleader of this sort of view".^[65] These approaches have been described as a revival of immaterialism^[66]

Relational quantum mechanics

The essential idea behind relational quantum mechanics, following the precedent of special relativity, is that different observers may give different accounts of the same series of events: for example, to one observer at a given point in time, a system may be in a single, "collapsed" eigenstate, while to another observer at the same time, it may be in a superposition of two or more states. Consequently, if quantum mechanics is to be a complete theory, relational quantum mechanics argues that the notion of "state" describes not the observed system itself, but the relationship, or correlation, between the system and its observer(s). The state vector of conventional quantum mechanics becomes a description of the correlation of some degrees of freedom in the observer, with respect to the observed system. However, it is held by relational quantum mechanics that this applies to all physical objects, whether or not they are conscious or macroscopic. Any "measurement event" is seen simply as an ordinary physical interaction, an establishment of the sort of correlation discussed above. Thus the physical content of the theory has to do not with objects themselves, but the relations between them.^[67][68]

An independent relational approach to quantum mechanics was developed in analogy with David Bohm's elucidation of special relativity,^[69] in which a detection event is regarded as establishing a relationship between the quantized field and the detector. The inherent ambiguity associated with applying Heisenberg's uncertainty principle is subsequently avoided.^[70]

Quantum Bayesianism

Interpretations where quantum mechanics is said to describe an observer's knowledge of the world, rather than the world itself. Quantum Bayesianism ("QBism") aims at giving a "subjective Bayesian account of quantum probability",^[71] to derive quantum mechanics from informational considerations.

This approach has some similarity with Bohr's thinking.^[72] Collapse (also known as reduction) is often interpreted as an observer acquiring information from a measurement, rather than as an objective event. These approaches have been appraised as similar to instrumentalism.^[73]

Other

Ensemble interpretation

The ensemble interpretation, or statistical interpretation can be viewed as a minimalist approach; it is a quantum mechanical interpretation that claims to make the fewest assumptions associated with the standard mathematical formalization. At its heart, it takes to the fullest extent the statistical Born rule.^[74]

It does not attempt to justify, or otherwise derive, or explain quantum mechanics from any deterministic process, or make any other statement about the real nature of quantum phenomena; it is simply a statement as to the manner of wave function interpretation. The wave function in this interpretation is not a property of any individual system, it is by its nature a statistical description of a hypothetical "ensemble" of similar systems. The probabilistic nature of quantum mechanical predictions thus follow directly from the construction or scope of the theory rather than from any intrinsic property of nature.

Probably the most notable supporter of such an interpretation was Albert Einstein:

The attempt to conceive the quantum-theoretical description as the complete description of the individual systems leads to unnatural theoretical interpretations, which become immediately unnecessary if one accepts the interpretation that the description refers to ensembles of systems and not to individual systems.

— Albert Einstein^[75]

A prominent advocate of the ensemble interpretation is Leslie E. Ballentine, Professor at Simon Fraser University, and writer of the graduate-level textbook Quantum Mechanics, a Modern Development.^[76]

Modal interpretations

Modal interpretations of quantum mechanics were first conceived of in 1972 by B. van Fraassen, in his paper "A formal approach to the philosophy of science." However, this term now is used to describe a class of models that grew out of this approach.

The Stanford Encyclopedia of Philosophy has an article on "Modal Interpretations of Quantum Mechanics"^[77] which presents "modal interpretations" as a class contrasting with objective collapse theories, pilot-wave theories and many-worlds interpretations.

Van Fraassen's proposal distinguished a dynamical state from a value state. The dynamical state corresponds to the ordinary quantum state, which however never collapses. The value state is the feature which replaces the idea of "collapse". An observable of a system is taken to have a sharp value even if the dynamical state is not an eigenstate of that same observable. Van Fraassen's proposal is "modal" because it leads to a modal logic of quantum propositions. Since the 1980s, a number of authors have developed other "realist" proposals which can in retrospect be classed with van Fraassen's "modal" proposal.

Consistent histories

The consistent histories interpretation is based on a consistency criterion that allows the history of a system to be described so that the probabilities for each history obey the additive rules of classical probability.

According to this interpretation, the purpose of a quantum-mechanical theory is to predict the relative probabilities of various alternative histories (for example, of a particle). It is claimed to be consistent with the Schrödinger equation. It attempts to provide a natural interpretation of quantum cosmology.

According to Robert E. Griffiths "It is in fact not necessary to interpret quantum mechanics in terms of measurements."^[78]

Nevertheless, Griffiths also says "A quantum theory of measurements is a necessary part of any consistent way of understanding quantum theory for a fairly obvious reason." Griffiths' explanation of this is that quantum measurement theory is derived from the principles of quantum mechanics, which, however, do not themselves explicitly postulate a primary ontological category of measurement in its own right, and which can be interpreted without explicit talk of measurement. Griffiths writes "Thus quantum measurements can, at least in principle, be analyzed using quantum theory."^[79] This contradicts the postulate of the orthodox interpretation, that the wave function changes in two ways, (1) according to the Schrödinger equation, which does not involve measurement, and (2) in the so-called 'collapse' or 'reduction' that occurs upon particle detection in the process of measurement.^[80]

Tabular comparison

The most common interpretations are summarized in the table below. The values shown in the cells of the table are not without controversy, for the precise meanings of some of the concepts involved are unclear and, in fact, are themselves at the center of the controversy surrounding the given interpretation.

No empirical evidence exists that distinguishes among these interpretations. To that extent, the physical theory stands, and is consistent within itself and with observation and experiment; difficulties arise only when one attempts to "interpret" the theory. Nevertheless, designing experiments which would test the various interpretations is the subject of active research.

Most of these interpretations have variants. For example, it is difficult to get a precise definition of the Copenhagen interpretation as it was developed and argued about by many people.

Interpretation	Author(s)	Deterministic?	Wavefunction real?	Unique history?	Hidden variables?	Collapsing wavefunctions?	Observer role?	Local?	Counterfactual definiteness?	Universal wavefunction exists?
Ensemble interpretation	Max Born, 1926	Agnostic	No	Yes	Agnostic	No	No	Agnostic	No	No
Hydrodynamic Interpretation	Erwin Madelung, 1926	Yes	Yes	Yes	Yes	No	No	No	Yes	Yes
Copenhagen interpretation	Niels Bohr, Werner Heisenberg, 1927	No	No1	Yes	No	Yes2	Causal	Agnostic	No	No
de Broglie–Bohm theory	Louis de Broglie, 1927, David Bohm, 1952	Yes	Yes3	Yes4	Yes	No	No	No17	Yes	Yes
von Neumann interpretation	John von Neumann, 1932, John Archibald Wheeler, Eugene Wigner	No	Yes	Yes	No	Yes	Causal	No	No	Yes
Quantum logic	Garrett Birkhoff, 1936	Agnostic	Agnostic	Yes5	No	No	Interpretational6	Agnostic	No	No
Time-symmetric theories	Olivier Costa de Beauregard, 1947, Satosi Watanabe, 1955	Yes	Yes	Yes	Yes	No	No	Yes	No	Yes
Many-worlds interpretation	Hugh Everett, 1957	Yes	Yes	No	No	No	No	Yes	No	Yes
Popper's interpretation[81]	Karl Popper, 1957[82]	No	Yes	Yes	Yes	No	No	(Yes)13	Yes	No
Stochastic mechanics	Edward Nelson, 1966	No	No	Yes	Yes16	No	No	No	Only for position 16	No
Scale relativity	Laurent Nottale,1992	No	No	Yes	Yes	No	No	No	Yes	No
Many-minds interpretation	H. Dieter Zeh, 1970	Yes	Yes	No	No	No	Interpretational7	Yes	No	Yes
Consistent histories	Robert B. Griffiths, 1984	Agnostic8	Agnostic8	No	No	No	Interpretational6	Yes	No	No
Objective collapse theories	Ghirardi–Rimini–Weber, 1986, Penrose interpretation, 1989	No	Yes	Yes	No	Yes	No	No	No	No
Transactional interpretation	John G. Cramer, 1986	No	Yes	Yes	No	Yes9	No	No14	Yes	No
Relational interpretation	Carlo Rovelli, 1994	Agnostic	No	Agnostic10	No	Yes11	Intrinsic12	Yes	No	No

• ¹ According to Bohr, the concept of a physical state independent of the conditions of its experimental observation does not have a well-defined meaning. According to Heisenberg the wavefunction represents a probability, but not an objective reality itself in space and time.
• ² According to the Copenhagen interpretation, the wavefunction collapses when a measurement is performed.
• ³ Both particle AND guiding wavefunction are real.
• ⁴ Unique particle history, but multiple wave histories.
• ⁵ But quantum logic is more limited in applicability than Coherent Histories.
• ⁶ Quantum mechanics is regarded as a way of predicting observations, or a theory of measurement.
• ⁷ Observers separate the universal wavefunction into orthogonal sets of experiences.
• ⁸ If wavefunction is real then this becomes the many-worlds interpretation. If wavefunction is less than real, but more than just information, then Zurek calls this the "existential interpretation".
• ⁹ In the TI the collapse of the state vector is interpreted as the completion of the transaction between emitter and absorber.
• ¹⁰ Comparing histories between systems in this interpretation has no well-defined meaning.
• ¹¹ Any physical interaction is treated as a collapse event relative to the systems involved, not just macroscopic or conscious observers.
• ¹² The state of the system is observer-dependent, i.e., the state is specific to the reference frame of the observer.
• ¹³ Since Popper holds both CFD and locality to be true, it is under dispute whether his view is an interpretation (which is what he claimed) or a modification of Quantum Mechanics (which is what many Physicists claim), and, in case of the latter, if it has been empirically refuted or not by Bell test experiments.
• ¹⁴ The transactional interpretation is explicitly non-local.
• ¹⁵ The assumption of intrinsic periodicity is an element of non-locality consistent with relativity as the periodicity varies in a causal way.
• ¹⁶ In the stochastic interpretation it's not possible to define velocities for particles, i.e. the paths are not smooth. Moreover, to know the motion of the particles at any moment, you have to know what the Markov process is. However, once we know the exact initial conditions and the Markov process, the theory is in fact a realistic interpretation of quantum mechanics; trajectories are continuous.
• ¹⁷ The kind of locality violated by the theory is the one assumed in deriving Bell inequalities. In particular, this kind non-locality is compatible with no signaling theorem and so with relativity.
• ¹⁸ The interpretation is compatible with the view of a deterministic world as a whole, but does not exclude indeterminism.
• ¹⁹ There are no hidden variables associated with the state of the quantum entity, but there are hidden variables associated with the measurement-interactions.

See also

Afshar experiment Bohr–Einstein debates Glossary of quantum philosophy Macroscopic quantum phenomena Minority interpretations of quantum mechanics Penrose interpretation

Path integral formulation Philosophical interpretation of classical physics Quantum gravity Quantum Reality Quantum Zeno effect

Sources

• Bub, J.; Clifton, R. (1996). "A uniqueness theorem for interpretations of quantum mechanics". Studies in History and Philosophy of Modern Physics 27B: 181–219. 
• Rudolf Carnap, 1939, "The interpretation of physics", in Foundations of Logic and Mathematics of the International Encyclopedia of Unified Science. University of Chicago Press.
• Dickson, M., 1994, "Wavefunction tails in the modal interpretation" in Hull, D., Forbes, M., and Burian, R., eds., Proceedings of the PSA 1" 366–76. East Lansing, Michigan: Philosophy of Science Association.
• --------, and Clifton, R., 1998, "Lorentz-invariance in modal interpretations" in Dieks, D. and Vermaas, P., eds., The Modal Interpretation of Quantum Mechanics. Dordrecht: Kluwer Academic Publishers: 9–48.
• Fuchs, Christopher, 2002, "Quantum Mechanics as Quantum Information (and only a little more)." arXiv:quant-ph/0205039
• -------- and A. Peres, 2000, "Quantum theory needs no ‘interpretation’", Physics Today.
• Herbert, N., 1985. Quantum Reality: Beyond the New Physics. New York: Doubleday. ISBN 0-385-23569-0.
• Hey, Anthony, and Walters, P., 2003. The New Quantum Universe, 2nd ed. Cambridge Univ. Press. ISBN 0-521-56457-3.
• Jackiw, Roman; Kleppner, D. (2000). "One Hundred Years of Quantum Physics". Science 289 (5481): 893. doi:10.1126/science.289.5481.893. 
• Max Jammer, 1966. The Conceptual Development of Quantum Mechanics. McGraw-Hill.
• --------, 1974. The Philosophy of Quantum Mechanics. Wiley & Sons.
• Al-Khalili, 2003. Quantum: A Guide for the Perplexed. London: Weidenfeld & Nicholson.
• de Muynck, W. M., 2002. Foundations of quantum mechanics, an empiricist approach. Dordrecht: Kluwer Academic Publishers. ISBN 1-4020-0932-1.^[83]
• Roland Omnès, 1999. Understanding Quantum Mechanics. Princeton Univ. Press.
• Karl Popper, 1963. Conjectures and Refutations. London: Routledge and Kegan Paul. The chapter "Three views Concerning Human Knowledge" addresses, among other things, instrumentalism in the physical sciences.
• Hans Reichenbach, 1944. Philosophic Foundations of Quantum Mechanics. Univ. of California Press.
• Tegmark, Max; Wheeler, J. A. (2001). "100 Years of Quantum Mysteries". Scientific American 284: 68. doi:10.1038/scientificamerican0201-68. 
• Bas van Fraassen, 1972, "A formal approach to the philosophy of science", in R. Colodny, ed., Paradigms and Paradoxes: The Philosophical Challenge of the Quantum Domain. Univ. of Pittsburgh Press: 303-66.
• John A. Wheeler and Wojciech Hubert Zurek (eds), Quantum Theory and Measurement, Princeton: Princeton University Press, ISBN 0-691-08316-9, LoC QC174.125.Q38 1983.

References

Further reading

Almost all authors below are professional physicists.

• David Z Albert, 1992. Quantum Mechanics and Experience. Harvard Univ. Press. ISBN 0-674-74112-9.
• John S. Bell, 1987. Speakable and Unspeakable in Quantum Mechanics. Cambridge Univ. Press, ISBN 0-521-36869-3. The 2004 edition (ISBN 0-521-52338-9) includes two additional papers and an introduction by Alain Aspect.
• Dmitrii Ivanovich Blokhintsev, 1968. The Philosophy of Quantum Mechanics. D. Reidel Publishing Company. ISBN 90-277-0105-9.
• David Bohm, 1980. Wholeness and the Implicate Order. London: Routledge. ISBN 0-7100-0971-2.
• Adan Cabello (15 November 2004). "Bibliographic guide to the foundations of quantum mechanics and quantum information". arXiv:quant-ph/0012089. 
• John G. Cramer, The Quantum Handshake: Entanglement, Nonlocality and Transactions, Springer Verlag 2015, ISBN 978-3-319-24640-6.
• David Deutsch, 1997. The Fabric of Reality. London: Allen Lane. ISBN 0-14-027541-X; ISBN 0-7139-9061-9. Argues forcefully against instrumentalism. For general readers.
• Bernard d'Espagnat, 1976. Conceptual Foundation of Quantum Mechanics, 2nd ed. Addison Wesley. ISBN 0-8133-4087-X.
• --------, 1983. In Search of Reality. Springer. ISBN 0-387-11399-1.
• --------, 2003. Veiled Reality: An Analysis of Quantum Mechanical Concepts. Westview Press.
• --------, 2006. On Physics and Philosophy. Princeton Univ. Press.
• Arthur Fine, 1986. The Shaky Game: Einstein Realism and the Quantum Theory. Science and its Conceptual Foundations. Univ. of Chicago Press. ISBN 0-226-24948-4.
• Ghirardi, Giancarlo, 2004. Sneaking a Look at God's Cards. Princeton Univ. Press.
• Gregg Jaeger (2009) Entanglement, Information, and the Interpretation of Quantum Mechanics. Springer. ISBN 978-3-540-92127-1.
• N. David Mermin (1990) Boojums all the way through. Cambridge Univ. Press. ISBN 0-521-38880-5.
• Roger Penrose, 1989. The Emperor's New Mind. Oxford Univ. Press. ISBN 0-19-851973-7. Especially chpt. 6.
• --------, 1994. Shadows of the Mind. Oxford Univ. Press. ISBN 0-19-853978-9.
• --------, 2004. The Road to Reality. New York: Alfred A. Knopf. Argues that quantum theory is incomplete.
• Styer, Daniel F.; Balkin, Miranda S.; Becker, Kathryn M.; Burns, Matthew R.; Dudley, Christopher E.; Forth, Scott T.; Gaumer, Jeremy S.; Kramer, Mark A.; et al. (March 2002). "Nine formulations of quantum mechanics". American Journal of Physics 70 (3): 288–297. Bibcode:2002AmJPh..70..288S. doi:10.1119/1.1445404. 

External links

Wikiversity has learning materials about Making sense of quantum mechanics

• Interpretations of Quantum Mechanics at the Internet Encyclopedia of Philosophy.
• Stanford Encyclopedia of Philosophy:
  • "Bohmian mechanics" by Sheldon Goldstein.
  • "Collapse Theories." by Giancarlo Ghirardi.
  • "Copenhagen Interpretation of Quantum Mechanics" by Jan Faye.
  • "Everett's Relative State Formulation of Quantum Mechanics" by Jeffrey Barrett.
  • "Many-Worlds Interpretation of Quantum Mechanics" by Lev Vaidman.
  • "Modal Interpretation of Quantum Mechanics" by Michael Dickson and Dennis Dieks.
  • "Quantum Entanglement and Information" by Jeffrey Bub.
  • "Quantum mechanics" by Jenann Ismael.
  • "Relational Quantum Mechanics" by Federico Laudisa and Carlo Rovelli.
  • "The Role of Decoherence in Quantum Mechanics" by Guido Bacciagaluppi.
• Willem M. de Muynck, Broad overview of the realist vs. empiricist interpretations, against oversimplified view of the measurement process.
• Schreiber, Z., "The Nine Lives of Schrodinger's Cat." Overview of competing interpretations.
• Interpretations of quantum mechanics on arxiv.org.
• The many worlds of quantum mechanics.
• Erich Joos' Decoherence Website.
• Quantum Mechanics for Philosophers. Argues for the superiority of the Bohm interpretation.
• Hidden Variables in Quantum Theory: The Hidden Cultural Variables of their Rejection.
• Numerous Many Worlds-related Topics and Articles.
• Relational Approach to Quantum Physics.
• Theory of incomplete measurements. Deriving quantum mechanics axioms from properties of acceptable measurements.
• Alfred Neumaier's FAQ.
• Measurement in Quantum Mechanics FAQ.
• "Quantum Mechanics - the dream stuff is made of" (September 2015)

Quantum mechanics Background Introduction Classical mechanics Old quantum theory Glossary History Fundamentals Bra–ket notation Complementarity Density matrix Hamiltonian Interference Decoherence Nonlocality Quantum state Superposition Tunnelling Scattering theory Symmetry in quantum mechanics Uncertainty Wave function Formulations Formulations Heisenberg Interaction Matrix mechanics Schrödinger Sum over histories Phase space Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger Interpretations Interpretations Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden variables Many-worlds Objective collapse Quantum logic Relational Stochastic Transactional Experiments Afshar Bell's inequality Cold Atom Laboratory Davisson–Germer Delayed choice quantum eraser Double-slit Franck–Hertz experiment Mach-Zehnder inter. Elitzur–Vaidman Popper Quantum eraser Schrödinger's cat Stern–Gerlach Wheeler's delayed choice Applications Quantum biology Quantum chemistry Quantum chaos Quantum cryptography Quantum electronics Quantum gravity Quantum machine Quantum mind Quantum optics Quantum field theory Quantum statistical mechanics Quantum information science Quantum technology Fractional quantum mechanics Relativistic quantum mechanics