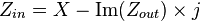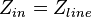Input impedance

The input impedance of an electrical network is the measure of opposition to static and dynamic current flow (impedance) from the electrical source into the load network being connected. If the source was disconnected from the load network and instead was connected to a device with an impedance equal to the input impedance of the load network it would produce the same voltage across and current through the input terminals as the original load network. Therefore, the input impedance of the network being connected and the output impedance of the source determines the transfer function from the source to the input terminals of the circuit.

The Thévenin's equivalent circuit of the electrical network uses the concept of input impedance to determine the impedance of the equivalent circuit.

Input impedance

If one were to create a circuit with equivalent properties across the input terminals by placing the input impedance across the load of the circuit and the output impedance in series with the signal source, Ohm's Law could be used to calculate the transfer function. To calculate the input impedance, short the input terminals together and reduce the circuit by determining the equivalent circuit with only one component.

Electrical Efficiency

The values of the input and output impedance are often used to evaluate the electrical efficiency of networks by breaking them up into multiple stages and evaluating the efficiency of the interaction between each stage interdependently. To minimize electrical losses, the output impedance of the signal should be insignificant in comparison to the input impedance of the network being connected as the gain is equivalent to the ratio of the input impedance to the total impedance (input impedance + output impedance). In this case,

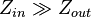
Z_{in} \gg Z_{out}
The input impedance of the driven stage (load) is much larger than the output impedance of the source.

Power factor

In AC circuits carrying power, the losses due to the reactive component of the impedance can be significant. These losses manifest themselves in a phenomenon called phase imbalance, where the current is out of phase (lagging behind or ahead of) the voltage. Therefore, the product of the current and the voltage is less than what it would be if the current and voltage were in phase. With DC sources, reactive circuits have no impact, therefore power factor correction is not necessary.

For a circuit modeled with an ideal source, an output impedance, and an input impedance; the circuits input reactance can be sized to be the negative of the output reactance of the load. In this scenario the reactive component of the input impedance cancels the reactive component of the output impedance of the load. From the ideal sources perspective the circuit between the output and input impedance is purely resistive in nature, and there are no losses due to phase imbalance in the source or the load.

\begin{align} Z_{in} & = X - \operatorname{Im}(Z_{out}) \times j \\ \end{align}

Power transfer

The maximum power will be transferred when the resistance of the source is equal to the resistance of the load and the power factor is corrected by canceling out the reactance. When this occurs the circuit is said to be complex conjugate matched to the signals impedance. Note this only maximizes the power transfer, not the efficiency of the circuit. When the power transfer is optimized the circuit only runs at 50% efficiency. Also note that this equation does not work in reverse, the optimal output impedance of the source is 0 regardless of the input impedance of the load.

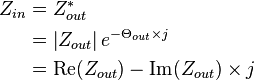
\begin{align} Z_{in} & = Z_{out}^* \\ & = \left\vert Z_{out} \right\vert e^{- \Theta_{out} \times j} \\ & = \operatorname{Re}(Z_{out}) - \operatorname{Im}(Z_{out}) \times j \\ \end{align}
When there is no reactive component this equation simplifies to 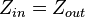Z_{in} = Z_{out} as the imaginary part of 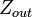Z_{out} is zero.

Impedance matching

To minimize reflections the characteristic impedance of the transmission line, and the load impedance have to be equal (or "matched"). Failure to match impedance will create standing waves on the transmission line due to reflections. This is known as a matched connection, and the process of correcting an impedance mismatch is called impedance matching.

Z_{in} = Z_{line}

Applications

Audio systems

Generally in audio and hi-fi systems, modern amplifier devices (such as Operational amplifiers) will have an input impedance several orders of magnitude higher than the output impedance of the source device connected to that input, for example: the output of another amplifier; the loading effects will be minimised - the voltage "seen" at the input will then be close to the unloaded output voltage (see EMF) of the source; this concept is also called voltage bridging or impedance bridging.

The input impedance for high-impedance amplifiers (such as vacuum tubes, Field Effect Transistor amplifiers and op-amps) is often specified as a resistance in parallel with a capacitance (e.g. 2.2 Megohms // 1 pF).

For signal sources such as transducers, the exact termination impedance of the input cable may be important, for example a gramophone pickup cartridge may specify 47 kilohms, and so the amplifier equipment's effective input resistance may be defined by a close-tolerance resistor at the input in parallel with a high impedance amplifier circuit which, although it may have an inaccurately-defined input impedance, has negligible effect on the overall impedance "seen" by the source.

Pre-amplifiers designed for high input impedance may have a slightly higher effective noise voltage at the input (while providing a low effective noise current), and so slightly more noisey than an amplifier designed for a specific low-impedance source, but in general a relatively low-impedance source configuration will be more resistant to noise (particularly mains hum).

In certain situations a voltage follower stage, or some other high-impedance amplifer circuit, is inserted between high-impedance source and an amplifier whose input impedance would be too low without the buffer stage. Sometimes an impedance-matching transformer can be used in place of a buffer amplifier (for example to match a low-voltage, low-impedance moving-coil pickup to an amplifer designed for a higher-impedance moving magnet type).

Video and high frequency (RF) systems

In RF systems, typical values for line and termination impedance are 50 Ω and 75 Ω. In analog video circuits, impedance mismatch can cause "ghosting", where the time-delayed echo of the principal image appears as a weak and displaced image (typically to the right of the principal image). In high-speed digital systems, such as HD video, reflections result in interference and potentially corrupt signal.

Radio frequency power systems

The standing waves created by the mismatch are periodic regions of higher than normal voltage. If this voltage exceeds the dielectric breakdown strength of the insulating material of the line then an arc will occur. This in turn can cause a reactive pulse of high voltage that can destroy the transmitter's final output stage. Signal reflections can result in distortion and potential damage to the driving circuitry.

To maximise power transmission for radio frequency power systems the circuits should be complex conjugate matched throughout the power chain, from the transmitter output, through the transmission line (a balanced pair, a coaxial cable, or a waveguide), to the antenna system, which consists of an impedance matching device and the radiating element(s).

In the case of purely resistive impedances (no reactive components), the two types of impedance matching are identical.

See also

External links

Sources

This article is issued from Wikipedia - version of the Monday, February 15, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.