Inex
The inex is an eclipse cycle of 10,571.95 days (about 29 years minus 20 days). The cycle was first described in modern times by Crommelin in 1901, but was named by George van den Bergh who studied it half a century later. It has been suggested that the cycle was known to Hipparchos.[1] A new saros series often begins one inex after the last series started.
It corresponds to:
- 358 lunations (synodic months)
- 388.50011 draconitic months
- 30.50011 eclipse years
- 383.67351 anomalistic months.
The 30.5 eclipse years means that if there is a solar eclipse (or lunar eclipse), then after one inex a New Moon (resp. Full Moon) will take place at the opposite node of the orbit of the Moon, and under these circumstances another eclipse can occur.
Unlike the saros, the inex is not close to an integer number of anomalistic months so successive eclipses are not very similar in their appearance and characteristics. From the remainder of 0.67351, being near 2⁄3, every third eclipse will have a similar position in the moon's elliptical orbit and apparent diameter, so the quality of the solar eclipse (total versus annular) will repeat in these groupings of 3 cycles (87 years minus 2 months), called triads.
Although the inex series lasts much longer than the saros, it is not unbroken: at the beginning and end of a series, eclipses may fail to occur. However once settled down, inex series are very stable and run for many thousands of years.
An inex also is close to an integer number of days (10,571.95) so solar eclipses on average take place at about the same geographical longitude at successive events, although variations of the moon's revolutionary speed at different points of the eclipse mask this relation. In addition sequential events occur at opposite geographical latitudes because the eclipses occur at opposite nodes. This is in contrast to the better known saros, which has a period of about 6,585 1⁄3 days, so successive solar eclipses tend to take place about 120° in longitude apart on the globe (although at the same node and hence at about the same geographical latitude).
The significance of the inex cycle is not in the prediction, but in the organization of eclipses: any eclipse cycle, and indeed the interval between any two eclipses, can be expressed as a combination of saros and inex intervals. Also when a saros series has terminated, then often one inex after the last eclipse of that saros series, the first eclipse of a new saros series occurs. This incoming and exiting of saros series separated by an interval of 29 years suggested the name for this cycle.
An example partial inex solar eclipse series
This eclipse is a part of the long period inex cycle, repeating at alternating nodes, every 358 synodic months (≈ 10,571.95 days, or 29 years minus 20 days). Their appearance and longitude are irregular due to a lack of synchronization with the anomalistic month (period of perigee). However, groupings of 3 inex cycles (≈ 87 years minus 2 months) comes close (≈ 1,151.02 anomalistic months), so eclipses are similar in these groupings.
 September 9, 1904 (Saros 133) |
 August 21, 1933 (Saros 134) |
 July 31, 1962 (Saros 135) |
 July 11, 1991 (Saros 136) |
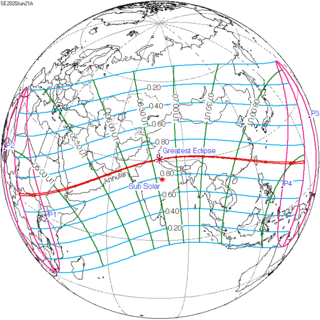 June 21, 2020 (Saros 137) |
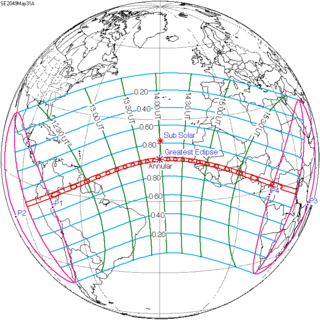 May 31, 2049 (Saros 138) |
 May 11, 2078 (Saros 139) |
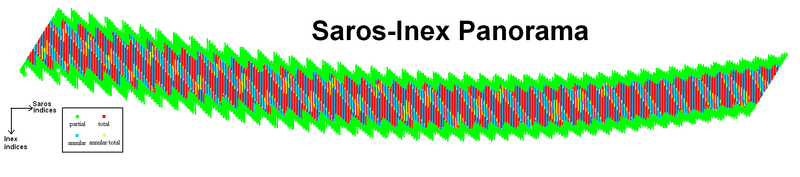
Solar Saros-Inex panorama
A saros-inex panorama has been produced by Luca Quaglia and John Tilley. It shows 61775 solar eclipses from −11000 (11001 BC) to +15000.[2]
Within each column of the graph is a complete Saros series which progresses smoothly from partial eclipses into total eclipses and back into partials. Each inex series extends as a graph row.
The lifetime and form of each inex series is not simple due to long term period variations: the synodic, draconic and anomalistic months.
 |
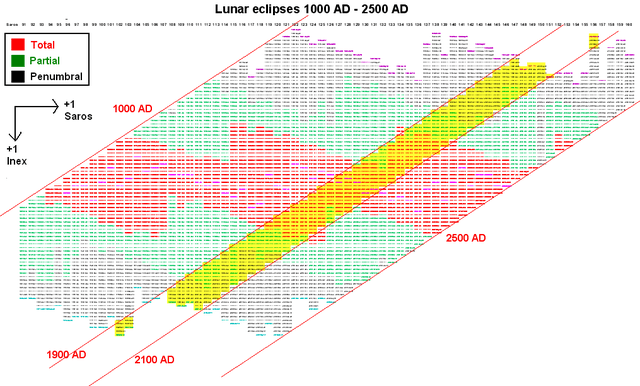
Lunar Saros-Inex panorama
Lunar eclipses can also be plotted in a similar diagram, this diagram covering 1000 AD to 2500 AD. The yellow diagonal band represents all the eclipses from 1900 to 2100. This graph immediately illuminates that this 1900–2100 period contains an above average number of total lunar eclipses compared to other adjacent centuries.
See also
- June_2058_lunar_eclipse#Inex_series – An example
References
- A.C.D. Crommelin (1901): The 29-year eclipse cycle. Observatory xxiv nr.310,379, Oct-1901
- G. van den Bergh (1954): Eclipses in the second millennium B.C. Tjeenk Willink & Zn NV, Haarlem 1954
- G. van den Bergh (1955): Periodicity and Variation of Solar (and Lunar) Eclipses, 2 vols. Tjeenk Willink & Zn NV, Haarlem 1955
- Mathematical Astronomy Morsels, Jean Meeus, Willmann-Bell, Inc., 1997 (Chapter 9, p. 51, Table 9. A Some eclipse Periodicities)