Inertial manifold
In mathematics, inertial manifolds are concerned with the long term behavior of the solutions of dissipative dynamical systems. Inertial manifolds are finite-dimensional, smooth, invariant manifolds that contain the global attractor and attract all solutions exponentially quickly. Since an inertial manifold is finite-dimensional even if the original system is infinite-dimensional, and because most of the dynamics for the system takes place on the inertial manifold, studying the dynamics on an inertial manifold produces a considerable simplification in the study of the dynamics of the original system.[1]
In many physical applications, inertial manifolds express an interaction law between the small and large wavelength structures. Some say that the small wavelengths are enslaved by the large (e.g. synergetics). Inertial manifolds may also appear as slow manifolds common in meteorology, or as the center manifold in any bifurcation. Computationally, numerical schemes for partial differential equations seek to capture the long term dynamics and so such numerical schemes form an approximate inertial manifold.
Introductory Example
Consider the dynamical system in just two variables  and
and 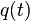 and with parameter
and with parameter  :[2]
:[2]
- It possesses the one dimensional inertial manifold
 of
of  (a parabola).
(a parabola). - This manifold is invariant under the dynamics because on the manifold
-
 which is the same as
which is the same as -
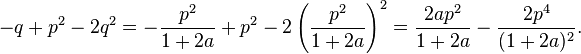
- The manifold
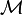 attracts all trajectories in some finite domain around the origin because near the origin
attracts all trajectories in some finite domain around the origin because near the origin 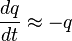 (although the strict definition below requires attraction from all initial conditions).
(although the strict definition below requires attraction from all initial conditions).
Hence the long term behavior of the original two dimensional dynamical system is given by the 'simpler' one dimensional dynamics on the inertial manifold 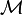 , namely
, namely  .
.
Definition
Let 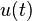 denote a solution of a dynamical system. The solution
denote a solution of a dynamical system. The solution 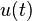 may be an evolving vector in
may be an evolving vector in  or may be an evolving function in an infinite-dimensional Banach space
or may be an evolving function in an infinite-dimensional Banach space  .
.
In many cases of interest the evolution of 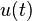 is determined as the solution of a differential equation in
is determined as the solution of a differential equation in  , say
, say  with initial value
with initial value 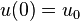 .
In any case, we assume the solution of the dynamical system can be written in terms of a semigroup operator, or state transition matrix,
.
In any case, we assume the solution of the dynamical system can be written in terms of a semigroup operator, or state transition matrix,  such that
such that  for all times
for all times 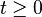 and all initial values
and all initial values  .
In some situations we might consider only discrete values of time as in the dynamics of a map.
.
In some situations we might consider only discrete values of time as in the dynamics of a map.
An inertial manifold[1] for a dynamical semigroup 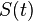 is a smooth manifold
is a smooth manifold 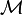 such that
such that
-
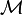 is of finite dimension,
is of finite dimension, -
 for all times
for all times 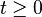 ,
, -
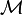 attracts all solutions exponentially quickly, that is, for every initial value
attracts all solutions exponentially quickly, that is, for every initial value  there exist constants
there exist constants 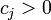 such that
such that 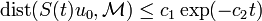 .
.
The restriction of the differential equation 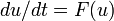 to the inertial manifold
to the inertial manifold 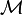 is therefore a well defined finite-dimensional system called the inertial system.[1]
Subtly, there is a difference between a manifold being attractive, and solutions on the manifold being attractive.
Nonetheless, under appropriate conditions the inertial system possesses so-called asymptotic completeness:[3] that is, every solution of the differential equation has a companion solution lying in
is therefore a well defined finite-dimensional system called the inertial system.[1]
Subtly, there is a difference between a manifold being attractive, and solutions on the manifold being attractive.
Nonetheless, under appropriate conditions the inertial system possesses so-called asymptotic completeness:[3] that is, every solution of the differential equation has a companion solution lying in 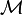 and producing the same behavior for large time; in mathematics, for all
and producing the same behavior for large time; in mathematics, for all  there exists
there exists  and possibly a time shift
and possibly a time shift 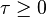 such that
such that  as
as  .
.
Researchers in the 2000s generalized such inertial manifolds to time dependent (nonautonomous) and/or stochastic dynamical systems (e.g.[4][5])
Existence
Existence results that have been proved address inertial manifolds that are expressible as a graph.[1]
The governing differential equation is rewritten more specifically in the form 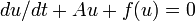 for unbounded self-adjoint closed operator
for unbounded self-adjoint closed operator  with domain
with domain  , and nonlinear operator
, and nonlinear operator 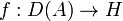 .
Typically, elementary spectral theory gives an orthonormal basis of
.
Typically, elementary spectral theory gives an orthonormal basis of  consisting of eigenvectors
consisting of eigenvectors  :
: 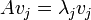 ,
,  , for ordered eigenvalues
, for ordered eigenvalues  .
.
For some given number  of modes,
of modes,  denotes the projection of
denotes the projection of  onto the space spanned by
onto the space spanned by  , and
, and  denotes the orthogonal projection onto the space spanned by
denotes the orthogonal projection onto the space spanned by 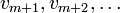 .
We look for an inertial manifold expressed as the graph
.
We look for an inertial manifold expressed as the graph 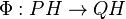 .
For this graph to exist the most restrictive requirement is the spectral gap condition[1]
.
For this graph to exist the most restrictive requirement is the spectral gap condition[1] 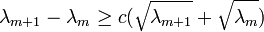 where the constant
where the constant  depends upon the system.
This spectral gap condition requires that the spectrum of
depends upon the system.
This spectral gap condition requires that the spectrum of  must contain large gaps to be guaranteed of existence.
must contain large gaps to be guaranteed of existence.
Approximate inertial manifolds
Several methods are proposed to construct approximations to inertial manifolds,[1] including the so-called intrinsic low-dimensional manifolds.[6][7]
The most popular way to approximate follows from the
existence of a graph.
Define the  slow
variables
slow
variables  , and the 'infinite'
fast variables
, and the 'infinite'
fast variables  .
Then project the differential equation
.
Then project the differential equation
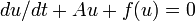 onto both
onto both 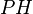 and
and 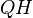 to obtain the coupled system
to obtain the coupled system
 and
and
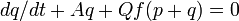 .
.
For trajectories on the graph of an inertial
manifold  , the fast
variable
, the fast
variable 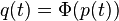 .
Differentiating and using the coupled system form gives the
differential equation for the graph:
.
Differentiating and using the coupled system form gives the
differential equation for the graph:
This differential equation is typically solved approximately
in an asymptotic expansion in 'small'  to
give an invariant manifold model,[8]
or a nonlinear Galerkin method,[9]
both of which use a global basis whereas the so-called
holistic discretisation uses a local basis.[10]
Such approaches to approximation of inertial manifolds are
very closely related to approximating center manifolds
for which a web service exists to construct approximations
for systems input by a
user.
to
give an invariant manifold model,[8]
or a nonlinear Galerkin method,[9]
both of which use a global basis whereas the so-called
holistic discretisation uses a local basis.[10]
Such approaches to approximation of inertial manifolds are
very closely related to approximating center manifolds
for which a web service exists to construct approximations
for systems input by a
user.
See also
References
- 1 2 3 4 5 6 R. Temam. Inertial manifolds. Mathematical Intelligencer, 12:68–74, 1990
- ↑ A. J. Roberts. Simple examples of the derivation of amplitude equations for systems of equations possessing bifurcations. J. Austral. Math. Soc. B, 27:48--65, 1985.
- ↑ J. C. Robinson. The asymptotic completeness of inertial manifolds. Nonlinearity, 9:1325–1340, 1996.
- ↑ B. Schmalfuss and K. R. Schneider. Invariant manifolds for random dynamical systems with slow and fast variables. Journal of Dynamics and Differential Equations, 20(1):133–164, 2008.
- ↑ C. Potzsche and M. Rasmussen. Computation of nonautonomous invariant and inertial manifolds. Numerische Mathematik, 112(3):449–483, 2009.
- ↑ U. Maas and S. B. Pope. Simplifying chemical kinetics: intrinsic low-dimensional manifolds in composition space. Combustion and Flame, 88:239–264, 1992.
- ↑ V. Bykov, I. Goldfarb, V. Goldshtein, and U. Maas. On a modified version of ILDM approach: asymptotic analysis based on integral manifolds. IMA Journal of Applied Mathematics, 71:359–382, 2006.
- ↑ A. J. Roberts. The utility of an invariant manifold description of the evolution of a dynamical system. SIAM J. Math. Anal., 20:1447–1458, 1989.
- ↑ C. Foias, M. S. Jolly, I. G. Kevrekidis, G. R. Sell, and E. S. Titi. On the computation of inertial manifolds. Phys. Lett. A, 131:433–436, 1988.
- ↑ A. J. Roberts. A holistic finite difference approach models linear dynamics consistently. Mathematics of Computation, 72:247–262, 2003.

![-\frac{d\Phi}{dp}\left[Ap+Pf(p+\Phi(p))\right]
+A\Phi(p)+Qf(p+\Phi(p))=0.](../I/m/53fa5f82b2f1cd46b3e7235dcde481b3.png)