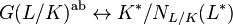Ramification group
In number theory, more specifically in local class field theory, the ramification groups are a filtration of the Galois group of a local field extension, which gives detailed information on the ramification phenomena of the extension.
Ramification groups in lower numbering
Ramification groups are a refinement of the Galois group  of a finite
of a finite 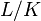 Galois extension of local fields. We shall write
Galois extension of local fields. We shall write 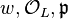 for the valuation, the ring of integers and its maximal ideal for
for the valuation, the ring of integers and its maximal ideal for  . As a consequence of Hensel's lemma, one can write
. As a consequence of Hensel's lemma, one can write ![\mathcal O_L = \mathcal O_K[\alpha]](../I/m/a981b4a66d1de2605fd5cacd4c201970.png) for some
for some 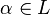 where
where  is the ring of integers of
is the ring of integers of 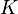 .[1] (This is stronger than the primitive element theorem.) Then, for each integer
.[1] (This is stronger than the primitive element theorem.) Then, for each integer  , we define
, we define  to be the set of all
to be the set of all 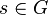 that satisfies the following equivalent conditions.
that satisfies the following equivalent conditions.
- (i)
 operates trivially on
operates trivially on 
- (ii)
 for all
for all 
- (iii)

The group  is called
is called  -th ramification group. They form a decreasing filtration,
-th ramification group. They form a decreasing filtration,
In fact, the  are normal by (i) and trivial for sufficiently large
are normal by (i) and trivial for sufficiently large  by (iii). For the lowest indices, it is customary to call
by (iii). For the lowest indices, it is customary to call 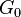 the inertia subgroup of
the inertia subgroup of  because of its relation to splitting of prime ideals, while
because of its relation to splitting of prime ideals, while  the wild inertia subgroup of
the wild inertia subgroup of  . The quotient
. The quotient  is called the tame quotient.
is called the tame quotient.
The Galois group  and its subgroups
and its subgroups  are studied by employing the above filtration or, more specifically, the corresponding quotients. In particular,
are studied by employing the above filtration or, more specifically, the corresponding quotients. In particular,
 where
where  are the (finite) residue fields of
are the (finite) residue fields of  .[2]
.[2] is unramified.
is unramified. is tamely ramified (i.e., the ramification index is prime to the residue characteristic.)
is tamely ramified (i.e., the ramification index is prime to the residue characteristic.)
The study of ramification groups reduces to the totally ramified case since one has  for
for  .
.
One also defines the function  . (ii) in the above shows
. (ii) in the above shows 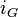 is independent of choice of
is independent of choice of  and, moreover, the study of the filtration
and, moreover, the study of the filtration  is essentially equivalent to that of
is essentially equivalent to that of 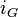 .[3]
.[3] 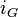 satisfies the following: for
satisfies the following: for 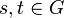 ,
,
Fix a uniformizer 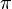 of
of  . Then
. Then  induces the injection
induces the injection  where
where  . (The map actually does not depend on the choice of the uniformizer.[4]) It follows from this[5]
. (The map actually does not depend on the choice of the uniformizer.[4]) It follows from this[5]
 is cyclic of order prime to
is cyclic of order prime to 
 is a product of cyclic groups of order
is a product of cyclic groups of order  .
.
In particular,  is a p-group and
is a p-group and  is solvable.
is solvable.
The ramification groups can be used to compute the different  of the extension
of the extension  and that of subextensions:[6]
and that of subextensions:[6]
If  is a normal subgroup of
is a normal subgroup of  , then, for
, then, for  ,
,  .[7]
.[7]
Combining this with the above one obtains: for a subextension  corresponding to
corresponding to 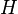 ,
,
If 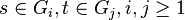 , then
, then  .[8] In the terminology of Lazard, this can be understood to mean the Lie algebra
.[8] In the terminology of Lazard, this can be understood to mean the Lie algebra  is abelian.
is abelian.
Example
Let K be generated by x1= . The conjugates of x1 are x2=
. The conjugates of x1 are x2= , x3= - x1, x4= - x2.
, x3= - x1, x4= - x2.
A little computation shows that the quotient of any two of these is a unit. Hence they all generate the same ideal; call it π. 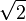 generates π2; (2)=π4.
generates π2; (2)=π4.
Now x1-x3=2x1, which is in π5.
and x1-x2=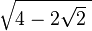 , which is in π3.
, which is in π3.
Various methods show that the Galois group of K is  , cyclic of order 4. Also:
, cyclic of order 4. Also:
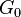 =
= =
= =
= .
.
and  =
= =(13)(24).
=(13)(24).
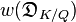 = 3+3+3+1+1 = 11. so that the different
= 3+3+3+1+1 = 11. so that the different  =π11.
=π11.
x1 satisfies x4-4x2+2, which has discriminant 2048=211.
Ramification groups in upper numbering
If 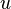 is a real number
is a real number  , let
, let  denote
denote  where i the least integer
where i the least integer 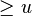 . In other words,
. In other words,  Define
Define 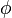 by[9]
by[9]
where, by convention,  is equal to
is equal to  if
if 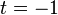 and is equal to
and is equal to 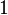 for
for 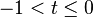 .[10] Then
.[10] Then  for
for  . It is immediate that
. It is immediate that 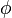 is continuous and strictly increasing, and thus has the continuous inverse function
is continuous and strictly increasing, and thus has the continuous inverse function 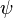 defined on
defined on  . Define
. Define
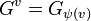 .
.
 is then called the v-th ramification group in upper numbering. In other words,
is then called the v-th ramification group in upper numbering. In other words,  . Note
. Note  . The upper numbering is defined so as to be compatible with passage to quotients:[11] if
. The upper numbering is defined so as to be compatible with passage to quotients:[11] if 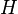 is normal in
is normal in  , then
, then
 for all
for all 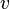
(whereas lower numbering is compatible with passage to subgroups.)
Herbrand's theorem states that the ramification groups in the lower numbering satisfy 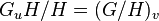 (for
(for 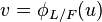 where
where  is the subextension corresponding to
is the subextension corresponding to 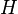 ), and that the ramification groups in the upper numbering satisfy
), and that the ramification groups in the upper numbering satisfy  .[12][13] This allows one to define ramification groups in the upper numbering for infinite Galois extensions (such as the absolute Galois group of a local field) from the inverse system of ramification groups for finite subextensions.
.[12][13] This allows one to define ramification groups in the upper numbering for infinite Galois extensions (such as the absolute Galois group of a local field) from the inverse system of ramification groups for finite subextensions.
The upper numbering for an abelian extension is important because of the Hasse–Arf theorem. It states that if  is abelian, then the jumps in the filtration
is abelian, then the jumps in the filtration  are integers; i.e.,
are integers; i.e.,  whenever
whenever  is not an integer.[14]
is not an integer.[14]
The upper numbering is compatible with the filtration of the norm residue group by the unit groups under the Artin isomorphism. The image of 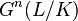 under the isomorphism
under the isomorphism
is just[15]
Notes
- ↑ Neukirch (1999) p.178
- ↑ since
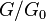 is canonically isomorphic to the decomposition group.
is canonically isomorphic to the decomposition group. - ↑ Serre (1979) p.62
- ↑ Conrad
- ↑ Use
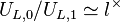 and
and 
- ↑ Serre (1979) 4.1 Prop.4, p.64
- ↑ Serre (1979) 4.1. Prop.3, p.63
- ↑ Serre (1979) 4.2. Proposition 10.
- ↑ Serre (1967) p.156
- ↑ Neukirch (1999) p.179
- ↑ Serre (1967) p.155
- ↑ Neukirch (1999) p.180
- ↑ Serre (1979) p.75
- ↑ Neukirch (1999) p.355
- ↑ Snaith (1994) pp.30-31
See also
References
- B. Conrad, Math 248A. Higher ramification groups
- Fröhlich, A.; Taylor, M.J. (1991). Algebraic number theory. Cambridge studies in advanced mathematics 27. Cambridge University Press. ISBN 0-521-36664-X. Zbl 0744.11001.
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, Zbl 0956.11021, MR 1697859
- Serre, Jean-Pierre (1967). "VI. Local class field theory". In Cassels, J.W.S.; Fröhlich, A. Algebraic number theory. Proceedings of an instructional conference organized by the London Mathematical Society (a NATO Advanced Study Institute) with the support of the International Mathematical Union. London: Academic Press. pp. 128–161. Zbl 0153.07403.
- Serre, Jean-Pierre (1979). Local Fields. Graduate Texts in Mathematics 67. Translated from the French by Marvin Jay Greenberg. Berlin, New York: Springer-Verlag. ISBN 0-387-90424-7. MR 0554237. Zbl 0423.12016.
- Snaith, Victor P. (1994). Galois module structure. Fields Institute monographs. Providence, RI: American Mathematical Society. ISBN 0-8218-0264-X. Zbl 0830.11042.