Indistinguishability quotient
The Sprague-Grundy theory of normal-play impartial combinatorial games generalizes to misere play via a local construction known as the indistinguishability quotient.
Suppose  is a set of impartial combinatorial games that is closed in both of the following senses:
is a set of impartial combinatorial games that is closed in both of the following senses:
(1) Additive closure: If  and
and 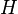 are games in
are games in  , then their disjunctive sum
, then their disjunctive sum
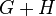 is also in
is also in  .
.
(2) Hereditary closure: If  is a game in
is a game in  and
and 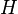 is an option of
is an option of  , then
, then
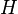 is also in
is also in  .
.
Next, define on  the indistinguishability congruence ≈ that relates two games
the indistinguishability congruence ≈ that relates two games  and
and 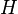 if for every choice of a game
if for every choice of a game  in
in  , the two positions
, the two positions 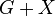 and
and 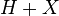 have the same outcome (i.e., are either both first-player wins in best play of
have the same outcome (i.e., are either both first-player wins in best play of  , or alternatively are both second-player wins).
, or alternatively are both second-player wins).
One easily checks that ≈ is indeed a congruence on the set of all disjunctive position sums in  , and that this is true regardless of whether the game is played in normal or misere play. The totality of all the congruence classes form the indistinguishability quotient.
, and that this is true regardless of whether the game is played in normal or misere play. The totality of all the congruence classes form the indistinguishability quotient.
If  is played as a normal-play (last-playing winning) impartial game, then the congruence classes of
is played as a normal-play (last-playing winning) impartial game, then the congruence classes of  are in one-to-one correspondence with the nim values that occur in the play of the game (themselves determined by the Sprague-Grundy theorem).
are in one-to-one correspondence with the nim values that occur in the play of the game (themselves determined by the Sprague-Grundy theorem).
In misere play, the congruence classes form a Monoid#Commutative monoid, instead, and it has become known as a misere quotient.
See also
References
- Plambeck, Thane E. (2005-07-19). "Taming the Wild in Impartial Combinatorial Games" (PDF). Integers: Electronic Journal of Combinatorial Number Theory (PDF) 5 (G05). Retrieved 2010-12-21.