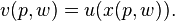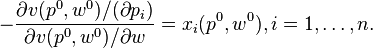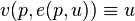Indirect utility function

In economics, a consumer's indirect utility function 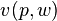gives the consumer's maximal attainable utility when faced with a vector of goods prices and an amount of income . It reflects both the consumer's preferences and market conditions.

This function is called indirect because consumers usually think about their preferences in terms of what they consume rather than prices. A consumer's indirect utility 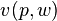can be computed from his or her utility function 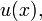defined over vectors of quantities of consumable goods, by first computing the most preferred affordable bundle, represented by the vector 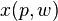by solving the utility maximization problem, and second, computing the utility 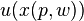the consumer derives from that bundle. The resulting indirect utility function is

The indirect utility function is:

• Continuous on Rⁿ₊₊+ R₊;
• Decreasing in prices;
• Strictly increasing in income;
• Homogenous with degree zero in prices and income; if prices and income are all multiplied by a given constant the same bundle of consumption represents a maximum, so optimal utility does not change.
• quasi convex in (p,w);

Moreover, Roy's identity states that if v(p,w) is differentiable at 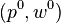and 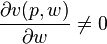, then

Indirect utility and expenditure

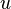The indirect utility function is the inverse of the expenditure function when the prices are kept constant. I.e, for every price vector and utility level :^[1]:106

See also

• Hicksian demand function
• Gorman polar form

References

• Mas-Colell, Andreu; Whinston, Michael D.; Green, Jerry R. (2007). Microeconomic Theory (Indian ed.). pp. 56–57. 
• Jehle, G. A.; Reny, P. J. (2011). Advanced Microeconomic Theory (Third ed.). Prentice Hall. pp. 28–33. 
• Nicholson, Walter (1978). Microeconomic Theory: Basic Principles and Extensions (Second ed.). Hinsdale: Dryden Press. pp. 57–59. ISBN 0-03-020831-9.