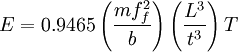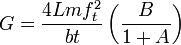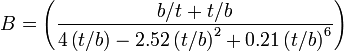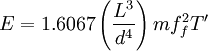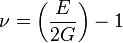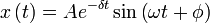Impulse excitation technique

The impulse excitation technique is a nondestructive test method that uses natural frequency, dimensions and mass of a test-piece to determine Young's modulus, Shear modulus, Poisson's ratio and damping coefficient.

Practical

Dimensions and mass of a test-piece can be easily measured. Natural frequency is determined by gently tapping the test-piece and analyzing the vibration. Tapping can be done using a small hammer or an automated tapping device. There are different ways to detect vibrations in the test-piece: piezoelectric sensor, microphone, laservibrometer or accelerometer. To optimize the results a microphone or a laservibrometer can be used as there is no contact between the test-piece and the sensor. Laservibrometers are preferred to measure signals with extreme frequencies. These kinds of signals are usually only induced in very thin test-pieces.

Flexure mode

Test-piece vibrating in flexure mode

This figure gives an example of a test-piece vibrating in the flexure mode. The induced vibration is also referred to as the out-of plane vibration. The in-plane vibration is the vibration vibrating vertically on the out-of plane vibration. The natural frequency of this vibration is measured to calculate Young's modulus. To damp the test-piece as little as possible it has to be supported at the nodes. The test-piece is mechanically excited at one of the anti-nodes to cause maximum vibration.

Torsion mode

Test-piece vibrating in the torsion mode

This figure gives an example of a test-piece vibrating in the torsion mode. The natural frequency of this vibration is measured to calculate the Shear modulus. To damp the test-piece as little as possible it has to be supported in the nodes. The test-piece is mechanically excited at one of the anti-nodes to cause maximum vibration.

Signal conditioning and calculating result

After the signal is induced it has to be amplified and filtered. The resulting signal can than be introduced in a software package where it is logged. Software packages use algorithms to calculate Young's modulus, Shear modulus, Poisson's ratio and damping coefficient. The basic formulas used in these algorithms are discussed in the theory section. Most software packages visualize the signal and show a graphic of the obtained frequencies.

Area of application

There is a wide range of untested applications in which impulse excitation techniques (IET) could be used. Today IET is mostly used in research and quality control. The advantage of IET in research projects is that it gives an in depth look into the internal structure of materials. Physical properties like damping and Young's modulus can be used for example to map out thermal shock behaviour of certain materials. Some machines even have the possibility to do measurements at very high temperatures, up to 1750 °C, or in vacuum conditions. This can be an advantage in understanding the physical properties of certain materials. Applications in quality control work differently. Most of these applications need a reference piece they can relate to. Engine blocks for example can be tested by tapping them and comparing the recorded signal with a pre-recorded signal of another engine block of which there is certainty its properties are satisfactory. From a material point of view most materials that have enough stiffness to vibrate can be measured using IET.

Theory

Rectangular bar

Young’s modulus

E = 0.9465\left( \frac{m f^2_f} {b} \right)\left( \frac{L^3} {t^3} \right)T

Where

T = 1+6.858\left( \frac{t} {L} \right)^2
E is Young's modulus
m is mass
ff is natural frequency in flexure dimension
b is width
L is length
t is thickness
The above formula can be used should L/t ≥ 20

Shear modulus

G = \frac{4Lmf_t^2} {bt}\left( \frac{B} {1+A} \right)

Where

B = \left( \frac{b/t + t/b} {4\left(t/b\right)-2.52\left(t/b\right)^2 + 0.21\left(t/b\right)^6} \right)
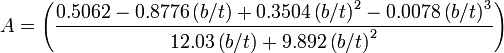
A = \left( \frac{0.5062 -0.8776\left( b/t\right) + 0.3504\left( b/t\right)^2- 0.0078\left( b/t\right)^3} {12.03\left(b/t\right)+9.892\left(b/t\right)^2} \right)
Note we assume that b≥t
ft is the natural frequency in the torsion mode
m is mass
b is width
L is length
t is thickness

Cylindrical rod

Young’s modulus

E = 1.6067\left( \frac{L^3} {d^4} \right)mf_f^2T'

Where

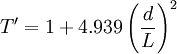
T' = 1+4.939\left( \frac{d} {L} \right)^2
E is Young's modulus
m is mass
ff is the natural frequency in flexure dimension
d is diameter
L is length
The above formula can be used should L/t ≥ 20

Shear modulus

G = 16 \left(\frac{L} {\pi d^2}\right)mf_t^2

Where

ft is the natural frequency in the torsion mode
m is mass
d is diameter
L is length

Poisson ratio

If Young's modulus and Shear modulus are known Poisson's ratio can be calculated.

\nu = \left(\frac{E} {2G}\right)-1

Damping coefficient

The signal induced in the test-piece is described as a damped sine. The damping of this sine can be determined by checking the force of consecutive amplitudes.

Damped sine
x\left(t\right) = Ae^{-\delta t}\sin\left(\omega t+\phi\right)

Where

f = 1/T = ω/(2π) the natural frequency
δ = kt the logarithmic decrement
k the exponential damping of the vibration signal

Accuracy

Accuracy is determined by the quality of support of the test-piece and the correctness of measurement of the test-piece’s dimensions and mass. It is possible to do measurements within an accuracy rate of 0,1%. The best way to support a test-piece is to use nylon fibers, but most systems use polyurethane foam strips as support. This makes it very difficult to measure small test-pieces because the damping effect of the support is too big.

Standards

External links

This article is issued from Wikipedia - version of the Saturday, March 14, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.