Impossible color

The human eye's red-to-green and blue-to-yellow values of each one-wavelength visible color

The CIE 1931 color space chromaticity diagram. The white regions correspond to imaginary colors.

The ProPhoto RGB color space uses imaginary green and blue primaries to obtain a larger gamut (space inside the triangle) than would be possible with three real primaries. However, some real colors are still irreproducible.

Normalized spectral sensitivity curves of the three kinds of cone cells, which define the space of human color sensation

Impossible colors or forbidden colors are supposed colors that cannot be perceived in normal seeing of light that is a combination of various intensities of the various frequencies of visible light, but are reported to be seen in special circumstances.

Types

These impossible colors are of two types:

1. Colors that would be seen if the output strengths of the human eye retina's three types of cone cell (red, green, blue) could be set to values which cannot be produced by exposing the eye in normal seeing conditions to any possible combination of strengths of the frequencies of visible light.
2. Colors that cannot be seen directly from any combination of retina signal output from one place in one eye, but can be generated in the brain's visual cortex by mixing color signals from the two eyes, or from more than one part of the same eye. Examples of these colors are bluish-yellow and reddish-green.^[1] Those colors that appear to be similar to, for example, both red and green, or to both yellow and blue. (This does not mean the result of mixing paints of those two colors in painting, or the result of mixing lights of those two colors on a screen.)

Opponent process

The color opponent process is a color theory that states that the human visual system interprets information about color by processing signals from cone and rod cells in an antagonistic manner. The three types of cone cells have some overlap in the wavelengths of light to which they respond, so it is more efficient for the visual system to record differences between the responses of cones, rather than each type of cone's individual response. The opponent color theory suggests that there are three opponent channels:

• Red versus green.
• Blue versus yellow
• Black versus white (this is achromatic and detects light-dark variation, or luminance).

Responses to one color of an opponent channel are antagonistic to those to the other color, and signals output from a place on the retina can contain one or the other but not both, for each opponent pair.

Real colors

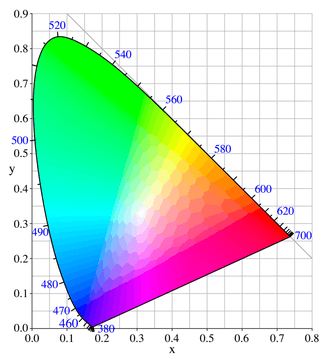
Real colors are colors that can be produced by a physical light source. Any additive mixture of two real colors is also a real color. When colors are displayed in the CIE 1931 XYZ color space, additive mixture results in a color along the line between the colors being mixed. By mixing any three colors, one can therefore create any color contained in the triangle they describe—this is called the gamut formed by those three colors, which are called primary colors. Any colors outside of this triangle cannot be obtained by mixing the chosen primaries.

When defining primaries, the goal is often to leave as many real colors in gamut as possible. Since the region of real colors is not a triangle (see illustration), it is not possible to pick three real colors that span the whole region. The gamut can be increased by selecting more than three real primary colors, but since the region of real colors is not a polygon, there always will be some colors at the edge left out. Therefore, one selects colors outside of the region of real colors as primary colors; in other words, imaginary primary colors. Mathematically, the gamut created in this way contains so-called "imaginary colors".

In computer and television screen color displays, the corners of the gamut triangle are defined by commercially available phosphors chosen to be as near as possible to pure red and pure green and pure blue, and thus are within the area of real colors; note that these color space diagrams inevitably display, instead of real colors outside your computer screen's gamut triangle, the nearest color which is inside the gamut triangle. See page Gamut for more information about the color range available on display devices.

Imaginary colors

One type of imaginary color (also referred to as non-physical or unrealizable color) is a point in a color space that corresponds to combinations of cone cell responses in one eye, that cannot be produced by the eye in normal circumstances seeing any possible light spectrum.^[2] Thus, no object can have an imaginary color. But such imaginary colors are useful as mathematical abstractions for defining color spaces.

The spectral sensitivity curve of medium-wavelength ("M") cone cells overlaps those of short-wavelength ("S") and long-wavelength ("L") cone cells. Light of any wavelength that interacts with M cones also interacts with S or L cones, or both, to some extent. Therefore, no wavelength (except perhaps a bit of the far red), and no non-negative spectral power distribution, excites only one sort of cone. If, for example, M cones could be excited alone, this would make the brain see an imaginary color greener than any physically possible green; producing it by seeing light would need some of the red and blue parts of visible light to have negative power, which is impossible. Such a "hyper-green" color would be in the CIE 1931 color space chromaticity diagram (left image to the right) in the blank area above the colored area and between the y-axis and the line x+y=1.

Chimerical colors

By staring at a "fatigue template" for 20-60 seconds, then switching to a neutral target, it is possible to view "impossible" colors.

A chimerical color is an imaginary color that can be seen temporarily by looking steadily at a strong color for a while until some of the cone cells become fatigued, temporarily changing their color sensitivities, and then looking at a markedly different color. They are explained by the opponent process color theory.^[3] For example, staring at a saturated primary-color field then looking at a white object results in an opposing shift in hue, causing an afterimage of the complementary colors. Exploration of the color space outside the range of "real colors" by this means is major corroborating evidence for the opponent process theory of color vision. Chimerical colors can be seen while seeing with one eye or with both eyes, and are not observed to reproduce simultaneously qualities of opposing colors (e.g. "yellowish blue").^[3] Chimerical colors include:

• Stygian colors: these are simultaneously dark and impossibly saturated. For example, to see "stygian blue": staring at bright yellow causes a dark blue afterimage, then on looking at black, the blue is seen as blue against the black, but due to lack of the usual brightness contrast it seems to be as dark as the black. The eye retina contains some neurons that fire only in the dark.
• Self-luminous colors: these mimic the effect of a glowing material, even when viewed on a medium such as paper, which can only reflect and not emit its own light. For example, to see "self-luminous red": staring at green causes a red afterimage, then on looking at white, the red is seen against the white and may seem to be brighter than the white.
• Hyperbolic colors: these are impossibly highly saturated. For example, to see "hyperbolic orange": staring at bright cyan causes an orange afterimage, then on looking at orange, the resulting orange afterimage seen against the orange background may cause an orange color purer than the purest orange color that can be made by any normally-seen light. Or, staring for two minutes at something pure magenta in bright sunlight for two minutes or more, and then looking at green leaves, may result in briefly seeing an unnaturally pure green afterimage.

Claimed evidence for ability to see impossible colors not in the color space

Some people may be able to see the color "yellow–blue" in this image by letting their eyes cross so that both + symbols are on top of each other

Under normal circumstances, there is no hue that one could describe as a mixture of opponent hues; that is, as a hue looking "redgreen" or "yellowblue".

In 1983, Hewitt D. Crane and Thomas P. Piantanida performed tests using an eye-tracker device that had a field of a vertical red stripe adjacent to a vertical green stripe, or several narrow alternating red and green stripes (or in some cases, yellow and blue instead). The device could track involuntary movements of one eye (there was a patch over the other eye) and adjust mirrors so the image would follow the eye and the boundaries of the stripes were always on the same places on the eye's retina; the field outside the stripes was blanked with occluders. Under such conditions, the edges between the stripes seemed to disappear (perhaps due to edge-detecting neurons becoming fatigued) and the colors flowed into each other in the brain's visual cortex, overriding the opponency mechanisms and producing not the color expected from mixing paints or from mixing lights on a screen, but new colors entirely, which are not in the CIE 1931 color space, either in its real part or in its imaginary parts. For red-and-green, some saw an even field of the new color; some saw a regular pattern of just-visible green dots and red dots; some saw islands of one color on a background of the other color. Some of the volunteers for the experiment reported that afterwards, they could still imagine the new colors for a period of time.^[1]

Some observers indicated that although they were aware that what they were viewing was a color (that is, the field was not achromatic), they were unable to name or describe the color. One of these observers was an artist with a large color vocabulary. Other observers of the novel hues described the first stimulus as a reddish-green.^[4]

In 2001 Vincent A. Billock and Gerald A. Gleason and Brian H. Tsou set up an experiment to test a theory that the 1983 experiment did not control for variations in the perceived luminance of the colors from subject to subject: two colors are equiluminant for an observer when rapidly alternating between the colors produces the least impression of flickering. The 2001 experiment was similar but controlled for luminance.^[5] They had these observations:

Some subjects (4 out of 7) described transparency phenomena—as though the opponent colors originated in two depth planes and could be seen, one through the other. ...

We found that when colors were equiluminant, subjects saw reddish greens, bluish yellows, or a multistable spatial color exchange (an entirely novel perceptual phenomena [sic]); when the colors were nonequiluminant, subjects saw spurious pattern formation.

This led them to propose a "soft-wired model of cortical color opponency", in which populations of neurons compete to fire and in which the "losing" neurons go completely silent. In this model, eliminating competition by, for instance, inhibiting connections between neural populations can allow mutually exclusive neurons to fire together.^[5]

Hsieh and Tse in 2006 disputed the existence of colors forbidden by opponency theory and claimed they are, in reality, intermediate colors.^[6] See also binocular rivalry.

In synesthetes

Some individuals with X → color synesthesia claim to be able to perceive impossible colors when, for example, two nearby letters have opposing colors. So, someone who has grapheme → color synesthesia, and who considers a to be red and n to be green might be able to perceive red-green if these two letters occur consecutively, like in the word an.

See also

• Bastard color: in theatre lighting, typically in a color gel, a color blended with small amounts of complementary colors.
• Color
• Color mixing
• Color vision
• False-color image, an image that depicts an object in colors that differ from those that a visible-colors-only photograph would show.
• Middle gray, a shade of gray used to adjust photographs to match perceptual brightness as opposed to absolute brightness as measured by a digital camera.
• Spectral color
• Tetrachromacy, having four primary colors
• Non-visible electromagnetic waves, such as radio waves, microwaves, X-rays, etc.
• List of fictional colors, mostly as seen by fictional aliens whose eyes work differently from human eyes.

References

• Imaginary Colors, Real Results, Dan Margulis, July, 2005

External links

• "Hyperbolic Orange and the River to Hell": blog about seeing "chimerical colors"

Further reading

• Billock, Vincent A.; Tsou, Brian H. (2010). "Seeing Forbidden Colors". Scientific American 302 (2): 72–7. doi:10.1038/scientificamerican0210-72. PMID 20128226. 
• Takahashi, Shigeko; Ejima, Yoshimichi (1984). "Spatial properties of red-green and yellow-blue perceptual opponent-color response". Vision Research 24 (9): 987–94. doi:10.1016/0042-6989(84)90075-0. PMID 6506487. 
• Hibino, H (1992). "Red-green and yellow-blue opponent-color responses as a function of retinal eccentricity". Vision Research 32 (10): 1955–64. doi:10.1016/0042-6989(92)90055-n. PMID 1287992.