Ignorance space

The ignorance space is the first component of the Bernoulli space which constitutes the stochastic model within Bernoulli stochastics.^[1] Ignorance means lack of knowledge about facts. Since Bernoulli Stochastics is a mathematical science, the facts refer to characteristics that are quantified by variables, and each fact is therefore represented by a unique real number. Because the considered variable has a fixed, i.e., determinate value, the variable is called deterministic variable denoted D. For example, consider a given object and let the characteristic of interest be the mass of the object. Then the deterministic variable D stands for mass which is quantified by the unit kilogram and for the object at hand D is fixed by a real number.

Ignorance, knowledge and truth

In the above example the mass of the object is fixed and the corresponding real number, say 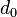$d_0$ specifies the value of D kilogram. The real number 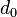$d_0$ constitutes the truth about the mass of the object. However, human beings are not able to determine the truth given by 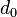$d_0$ , since whatever measurement device is used, the measurement process is subject to randomness and the determination of the true value 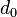$d_0$ of the deterministic variable D is in principle impossible.

It follows that human beings in general cannot know "what is", for example, the true value 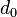$d_0$ . But, they can, of course know "what is not" since any weighing device yields a more or less small set 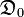$\mathfrak{D}_0$ which contains the true but unknown value 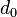$d_0$ . Thus human knowledge generally refers to "what is not" namely all numbers which are not contained in 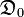$\mathfrak{D}_0$ , but it remains unknown which of the elements of 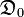$\mathfrak{D}_0$ is the true one.

Thus, human ignorance refers to truth, i.e., "what is", while human knowledge refers "what is not". The set 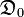$\mathfrak{D}_0$ describes therefore the state of ignorance about the true value 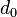$d_0$ of the deterministic variable D. Therefore the set 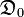$\mathfrak{D}_0$ is called ignorance space of D denoted 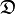$\mathfrak{D}$ .^[2]

Learning and ignorance space

Any reduction of an ignorance space 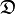$\mathfrak{D}$ represents the result of a learning process. In order to obtain a quantified description of a learning process, the ignorance space must be specified before the learning process is performed. Moreover, for judging the achieved result of a learning process, the hopefully reduced ignorance space must be given.

Whenever the truth is given by a real number, say 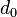$d_0$ , then a learning process is generally called measurement procedure or in case that it is based on a Bernoulli Space it is called stochastic measurement procedure. Measurement and learning are probably the most important activities of mankind and it is therefore of utmost importance that measurement and learning are performed in a rational and effective way in order to avoid or at least reduce waste of resources.

References

↑ Elart von Collani (ed.), Defining the Science Stochastics, Heldermann Verlag, Lemgo, 2004.
↑ Elart von Collani, Defining and medelling uncertainty, Journal of Uncertain Systems, Vol. 2, 202–211, 2008, .

External links

Stochastikon Ecyclopedia,
E-Learning Programme Stochastikon Magister,
Homepage of Stochastikon GmbH,
Economic Quality Control,

This article is issued from Wikipedia - version of the Sunday, November 15, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.