Hypertranscendental number
A complex number is said to be hypertranscendental if it is not the value at an algebraic point of a function which is the solution of an algebraic differential equation with coefficients in Z[r] and with algebraic initial conditions.
The term was introduced by D. D. Morduhai-Boltovskoi in "Hypertranscendental numbers and hypertranscendental functions" (1949).
The term is related to transcendental numbers, which are numbers which are not a solution of a non-zero polynomial equation with rational coefficients. The number e is transcendental but not hypertranscendental, as it can be generated from the solution to the differential equation 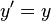 .
.
Any hypertranscendental number is also a transcendental number.
See also
References
- Mordukhai-Boltovskoi, Dmitrii Dmitrievich (1949). "[Hypertranscendental numbers and hypertranscendental functions]". Doklady Akademii Nauk SSSR 64: 21–24.
- Hiroshi Umemura, "On a class of numbers generated by differential equations related with algebraic groups", Nagoya Math. Journal. Volume 133 (1994), 1-55. (Downloadable from ProjectEuclid)
This article is issued from Wikipedia - version of the Tuesday, December 03, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.