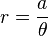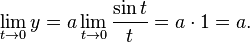Hyperbolic spiral

Hyperbolic spiral for a=2

A hyperbolic spiral is a transcendental plane curve also known as a reciprocal spiral.[1] A hyperbolic spiral is the opposite of an Archimedean spiral[2] and is a type of Cotes' spiral.

Pierre Varignon first studied the curve in 1704.[2] Later Johann Bernoulli and Roger Cotes worked on the curve as well.

Equation

The hyperbolic spiral has the polar equation:

r=\frac{a}{\theta}

It begins at an infinite distance from the pole in the center (for θ starting from zero r = a/θ starts from infinity), and it winds faster and faster around as it approaches the pole; the distance from any point to the pole, following the curve, is infinite. Applying the transformation from the polar coordinate system:

x = r \cos \theta, \qquad y = r \sin \theta,

leads to the following parametric representation in Cartesian coordinates:

x = a {\cos t \over t}, \qquad y = a {\sin t \over t},

where the parameter t is an equivalent of the polar coordinate θ.

Properties

Asymptote

The spiral has an asymptote at y = a: for t approaching zero the ordinate approaches a, while the abscissa grows to infinity:

\lim_{t\to 0}x = a\lim_{t\to 0}{\cos t \over t}=\infty,
\lim_{t\to 0}y = a\lim_{t\to 0}{\sin t \over t}=a\cdot 1=a.

Curvature

Using the representation of the hyperbolic spiral in polar coordinates, the curvature can be found by

\kappa = {r^2 + 2r_\theta^2 - r r_{\theta \theta} \over (r^2+r^2_\theta)^{3/2}}

where

r_\theta = {d r \over d \theta} = {-a \over \theta^2}

and

r_{\theta \theta} = {d^2 r \over d \theta^2} = {2 a \over \theta^3}.

Then the curvature at \theta reduces to

\kappa(\theta) = {\theta^4 \over a (\theta^2 + 1)^{3/2}}.

The curvature tends to infinity as \theta tends to infinity. For values of \theta between 0 and 1, the curvature increases exponentially, and for values greater than 1, the curvature increases at an approximately linear rate with respect to the angle.

Tangents

The tangential angle of the hyperbolic curve is

\phi(\theta) = -\tan^{-1} \theta.

References

  1. ↑ Bowser, Edward Albert (1880), An Elementary Treatise on Analytic Geometry: Embracing Plane Geometry and an Introduction to Geometry of Three Dimensions (4th ed.), D. Van Nostrand, p. 232.
  2. 1 2 Lawrence, J. Dennis (2013), A Catalog of Special Plane Curves, Dover Books on Mathematics, Courier Dover Publications, p. 186, ISBN 9780486167664.

External links

This article is issued from Wikipedia - version of the Thursday, March 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.