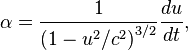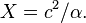Hyperbolic motion (relativity)
Hyperbolic motion is the motion of an object with constant proper acceleration in special relativity. It is called hyperbolic motion because the equation describing the path of the object through spacetime is a hyperbola, as can be seen when graphed on a Minkowski diagram.
The proper acceleration  of a particle is defined as the acceleration that a particle "feels" as it accelerates from one inertial reference frame to another. This can be derived mathematically as
of a particle is defined as the acceleration that a particle "feels" as it accelerates from one inertial reference frame to another. This can be derived mathematically as
where 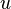 is the instantaneous speed of the particle,
is the instantaneous speed of the particle,  is the speed of light, and
is the speed of light, and  is time. Solving for the equation of motion results in
is time. Solving for the equation of motion results in
which is a hyperbola in time and the spatial location variable 
Hyperbolic motion is easily visualized on a Minkowski diagram, where the motion of the accelerating particle is along the  -axis. Each hyperbola is defined by
-axis. Each hyperbola is defined by
See also
References
- Born, M. (1909). "Die Theorie des starren Elektrons in der Kinematik des Relativitäts-Prinzipes". Ann. Phys. 30: 1. Bibcode:1909AnP...335....1B. doi:10.1002/andp.19093351102.
- Wikisource translation: The Theory of the Rigid Electron in the Kinematics of the Principle of Relativity
- Leigh Page (Feb 1936). "A New Relativity. Paper I. Fundamental Principles and Transformations Between Accelerated Systems". Physical Review 49 (3): 254–268. Bibcode:1936PhRv...49..254P. doi:10.1103/PhysRev.49.254.
- Leigh Page & Norman I. Adams (Mar 1936). "A New Relativity. Paper II. Transformation of the Electromagnetic Field Between Accelerated Systems and the Force Equation". Physical Review 49 (6): 466–469. Bibcode:1936PhRv...49..466P. doi:10.1103/PhysRev.49.466.
- Ludwik Silberstein (1914) The Theory of Relativity, page 190.
- Naber, Gregory L., The Geometry of Minkowski Spacetime, Springer-Verlag, New York, 1992. ISBN 0-387-97848-8 (hardcover), ISBN 0-486-43235-1 (Dover paperback edition). pp 58-60.