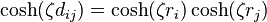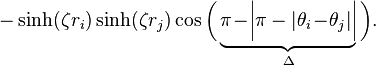Hyperbolic geometric graph
| Network science | ||||
|---|---|---|---|---|
| Network types | ||||
| Graphs | ||||
|
||||
| Models | ||||
|
||||
| ||||
|
||||
A hyperbolic geometric graph (HGG) or hyperbolic geometric network (HGN) is special spatial network where nodes are (1) sprinkled according to a probability distribution onto a hyperbolic space of constant negative curvature and (2) an edge between two nodes is present if they are close according to a function of the metric,[1][2] a HGG generalizes a random geometric graph (RGG) whose embedding space is Euclidean.
Mathematical formulation
Mathematically, a HGG is a graph 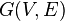 with a vertex set V (cardinality
with a vertex set V (cardinality 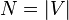 ) and a edge set E constructed by considering the nodes as points placed onto a 2-dimensional hyperbolic space
) and a edge set E constructed by considering the nodes as points placed onto a 2-dimensional hyperbolic space 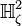 of constant negative Gaussian curvature,
of constant negative Gaussian curvature, 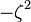 and cut-off radius
and cut-off radius  , i.e. the radius of the Poincaré disk which can be visualized using a hyperboloid model.
Each point
, i.e. the radius of the Poincaré disk which can be visualized using a hyperboloid model.
Each point  has hyperbolic polar coordinates
has hyperbolic polar coordinates 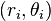 with
with 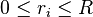 and
and 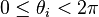 .
.
The hyperbolic law of cosines allows to measure the distance  between two points
between two points  and
and 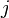 ,[2]
,[2]
The angle 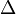 is the (smallest) angle between the two
position vectors.
is the (smallest) angle between the two
position vectors.
In the simplest case, an edge  is established iff (if and only if) two nodes are within a certain neighborhood radius
is established iff (if and only if) two nodes are within a certain neighborhood radius  ,
, 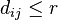 , this corresponds to an influence threshold.
, this corresponds to an influence threshold.
Connectivity decay function
In general, a link will be established with a probability depending on the distance  .
A connectivity decay function
.
A connectivity decay function ![\gamma(s): \mathbb{R}^+\to[0,1]](../I/m/a7a7120ce0cf290f35e9b2f7742929f0.png) represents the probability of assigning an edge to a pair of nodes at distance
represents the probability of assigning an edge to a pair of nodes at distance  .
In this framework, the simple case of hard-code neighborhood like in random geometric graphs is referred to as truncation decay function.[3]
.
In this framework, the simple case of hard-code neighborhood like in random geometric graphs is referred to as truncation decay function.[3]
Findings
For 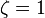 (Gaussian curvature
(Gaussian curvature 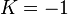 ), HGGs form an ensemble of networks for which is possible to express the degree distribution analytically as closed form for the limiting case of large number of nodes.[2] This is worth mentioning since this is not true for many ensemble of graphs.
), HGGs form an ensemble of networks for which is possible to express the degree distribution analytically as closed form for the limiting case of large number of nodes.[2] This is worth mentioning since this is not true for many ensemble of graphs.
Applications
HGGs have been suggested as promising model for social networks where the hyperbolicity appears through a competition between similarity and popularity of an individual.[4]
References
- ↑ Barthélemy, Marc. "Spatial networks". Physics Reports 499 (1-3): 1–101. doi:10.1016/j.physrep.2010.11.002. Retrieved 16 October 2014.
- 1 2 3 Krioukov, Dmitri; Papadopoulos, Fragkiskos; Kitsak, Maksim; Vahdat, Amin; Boguñá, Marián. "Hyperbolic geometry of complex networks". Physical Review E 82 (3). doi:10.1103/PhysRevE.82.036106.
- ↑ Barnett, L.; Di Paolo, E.; Bullock, S. "Spatially embedded random networks". Physical Review E 76 (5). doi:10.1103/PhysRevE.76.056115.
- ↑ Papadopoulos, Fragkiskos; Kitsak, Maksim; Serrano, M. Ángeles; Boguñá, Marián; Krioukov, Dmitri (12 September 2012). "Popularity versus similarity in growing networks". Nature 489 (7417): 537–540. doi:10.1038/nature11459. Retrieved 16 October 2014.