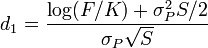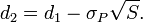Hull–White model
In financial mathematics, the Hull–White model is a model of future interest rates. In its most generic formulation, it belongs to the class of no-arbitrage models that are able to fit today's term structure of interest rates. It is relatively straightforward to translate the mathematical description of the evolution of future interest rates onto a tree or lattice and so interest rate derivatives such as bermudan swaptions can be valued in the model.
The first Hull–White model was described by John C. Hull and Alan White in 1990. The model is still popular in the market today.
The model
One-factor model
The model is a short-rate model. In general, it has dynamics
There is a degree of ambiguity amongst practitioners about exactly which parameters in the model are time-dependent or what name to apply to the model in each case. The most commonly accepted hierarchy has
- θ and α constant – the Vasicek model
- θ has t dependence – the Hull-White model
- θ and α also time-dependent – the extended Vasicek model
Two-factor model
The two-factor Hull–White model (Hull 2006:657–658) contains an additional disturbance term whose mean reverts to zero, and is of the form:
where  has an initial value of 0 and follows the process:
has an initial value of 0 and follows the process:
Analysis of the one-factor model
For the rest of this article we assume only  has t-dependence.
Neglecting the stochastic term for a moment, notice that the change in r is negative if r is currently "large" (greater than θ(t)/α) and positive if the current value is small. That is, the stochastic process is a mean-reverting Ornstein–Uhlenbeck process.
has t-dependence.
Neglecting the stochastic term for a moment, notice that the change in r is negative if r is currently "large" (greater than θ(t)/α) and positive if the current value is small. That is, the stochastic process is a mean-reverting Ornstein–Uhlenbeck process.
θ is calculated from the initial yield curve describing the current term structure of interest rates. Typically α is left as a user input (for example it may be estimated from historical data). σ is determined via calibration to a set of caplets and swaptions readily tradeable in the market.
When  ,
,  , and
, and 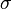 are constant, Itô's lemma can be used to prove that
are constant, Itô's lemma can be used to prove that
which has distribution
where  is the normal distribution with mean
is the normal distribution with mean 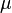 and variance
and variance  .
.
When 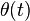 is time dependent,
is time dependent,
which has distribution
Bond pricing using the Hull–White model
It turns out that the time-S value of the T-maturity discount bond has distribution (note the affine term structure here!)
where
Note that their terminal distribution for P(S,T) is distributed log-normally.
Derivative pricing
By selecting as numeraire the time-S bond (which corresponds to switching to the S-forward measure), we have from the fundamental theorem of arbitrage-free pricing, the value at time 0 of a derivative which has payoff at time S.
Here, 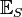 is the expectation taken with respect to the forward measure. Moreover that standard arbitrage arguments show
that the time T forward price
is the expectation taken with respect to the forward measure. Moreover that standard arbitrage arguments show
that the time T forward price 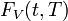 for a payoff at time T given by V(T) must satisfy
for a payoff at time T given by V(T) must satisfy 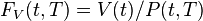 , thus
, thus
Thus it is possible to value many derivatives V dependent solely on a single bond P(S,T) analytically when working in the Hull–White model. For example in the case of a bond put
Because P(S,T) is lognormally distributed, the general calculation used for Black-Scholes shows that
where
and
Thus today's value (with the P(0,S) multiplied back in) is:
Here σP is the standard deviation of the log-normal distribution for P(S,T). A fairly substantial amount of algebra shows that it is related to the original parameters via
Note that this expectation was done in the S-bond measure, whereas we did not specify a measure at all for the original Hull-White process. This does not matter — the volatility is all that matters and is measure-independent.
Because interest rate caps/floors are equivalent to bond puts and calls respectively, the above analysis shows that caps and floors can be priced analytically in the Hull–White model. Jamshidian's trick applies to Hull-White (as today's value of a swaption in HW is a monotonic function of today's short rate). Thus knowing how to price caps is also sufficient for pricing swaptions.
The swaptions can also be priced directly as described in Henrard (2003). The direct implementation is usually more efficient.
Trees and lattices
However, valuing vanilla instruments such as caps and swaptions is useful primarily for calibration. The real use of the model is to value somewhat more exotic derivatives such as bermudan swaptions on a lattice, or other derivatives in a multi-currency context such as Quanto Constant Maturity Swaps, as explained for example in Brigo and Mercurio (2001).
See also
References
Primary references
- John Hull and Alan White, "Using Hull-White interest rate trees," Journal of Derivatives, Vol. 3, No. 3 (Spring 1996), pp 26–36
- John Hull and Alan White, "Numerical procedures for implementing term structure models I," Journal of Derivatives, Fall 1994, pp 7–16
- John Hull and Alan White, "Numerical procedures for implementing term structure models II," Journal of Derivatives, Winter 1994, pp 37–48
- John Hull and Alan White, "The pricing of options on interest rate caps and floors using the Hull–White model" in Advanced Strategies in Financial Risk Management, Chapter 4, pp 59–67.
- John Hull and Alan White, "One factor interest rate models and the valuation of interest rate derivative securities," Journal of Financial and Quantitative Analysis, Vol 28, No 2, (June 1993) pp 235–254
- John Hull and Alan White, "Pricing interest-rate derivative securities", The Review of Financial Studies, Vol 3, No. 4 (1990) pp. 573–592
Other references
- Hull, John C. (2006). "Interest Rate Derivatives: Models of the Short Rate". Options, Futures, and Other Derivatives (6th ed.). Upper Saddle River, N.J: Prentice Hall. pp. 657–658. ISBN 0-13-149908-4. LCCN 2005047692. OCLC 60321487.
- Damiano Brigo, Fabio Mercurio (2001). Interest Rate Models — Theory and Practice with Smile, Inflation and Credit (2nd ed. 2006 ed.). Springer Verlag. ISBN 978-3-540-22149-4.
- Henrard, Marc (2003). Explicit Bond Option and Swaption Formula in Heath-Jarrow-Morton One Factor Model, International Journal of Theoretical and Applied Finance, 6(1), 57-72. Preprint SSRN.
- Henrard, Marc (2009). Efficient swaptions price in Hull-White one factor model, arXiv, 0901.1776v1. Preprint arXiv.
- Eugen Puschkarski, Implementation of Hull-White´s No-Arbitrage Term Structure Model, Diploma Thesis, Center for Central European Financial Markets
- Letian Wang, Hull-White Model, Fixed Income Quant Group, DTCC (detailed numeric example and derivation)
Online utilities
- Hull-White Trinomial Tree, Dr. S.H. Man, Turaz.
- Short Rates Simulation using Hull White Model, Dr. S.H. Man, Turaz.
| ||||||||||||||||||||||||||||||
[1]مدل هال -وایت
از[2] ویکیپدیا، دانشنامه آزاد
در ریاضیات مالی، مدل هال-وایت ، مدلی برای نرخ های بهره ی آتی است .
در بسیاری از فرمول های عمومی اش، آن را متعلق به رده ی مدل های بدون آربیتراژ که قادر به متناسب کردن اصطلاحات ترکیبی امروزی نرخ بهره است می دانند.
تفسیر شرح ریاضی این مدل از تغییرات نرخ بهره ی آتی بر روی یک درخت و یا شبکه نسبتا ساده است وهمچنین مشتقات نرخ بهره مانند[3] سوپشن برمودا را می توان با این مدل سنجید.
مدل هال -وایت برای اولین بار توسط [4]جان سی هال و آلن وایت در سال 1990 ارائه شد. مدل هنوز هم در بازار امروز رایج است.
فهرست
1 مدل
1.1 مدل یک عامله
1.2 مدل دو عامله
2 تحلیل مدل یک عامله
3 قیمت گذاری اوراق قرضه با استفاده از مدل هال وایت
4 قیمت گذاری اشتفاقی
5 درختان و شبکه ها
6 جستارها
7 منابع
مدل
'[5]'مدل یک عامله
این مدل یک [6]مدل کوتاه نرخ است. به طور کلی، این مدل پویایی دارد:
درجه ای از ابهام در میان [7]شاغلان وجود دارد درباره ی این که دقیقا کدام پارامترها در مدل وابسته به زمان اند و یا چه نامی برای هر مورد ازمدل اعمال شود.
رایج ترین سلسله مراتب پذیرفته شده عبارت است از
و مقدار ثابت -مدل [8]وسیچک
وابسته به– مدل هال وایت
همچنین و وابسته به زمان - مدل [9]تعمیم یافته ی وسیچک
'مدل دو عامله[10]'
مدل دو عامله ی هال وایت(هال 2006: 657-658) شامل اصطلاح اختلال اضافی است که به معنای برگشت به صفراست، وبه فرم زیر است:
که در آن مقدار اولیه 0 و از روند زیر پیروی می کند:
تحلیل مدل یک عامله
در ادامه ی این گفتار ما فرض می کنیم فقط وابستگی تی وجود دارد .
عدم توجه به دوره ی تصادفی برای یک لحظه، توجه کنید که تغییر در Rمنفی است اگر R در حال حاضر "بزرگ" باشد .(بیشتر از θ(T) /α) و مثبت است اگر ارزش فعلی کوچک باشد .
که این یک فرایند تصادفی [11]میانگین بازگرداندن روند [12]اورنستین-اولن بک است.
θ از اولین خروجی منحنی توصیف ساختار بازده[13] حال حاضر ازنرخ بهره ،محاسبه شده است.
به طور معمول در سمت چپ به عنوان ورودی کاربر در نظر گرفته شده است، (برای مثال ممکن است از داده های تاریخی برآورد شود).
σ تعریف شده از طریق رتبه بندی به مجموعه ای از [14]کپلیت ها و سواپشن ها که به آسانی در بازار قابل معامله اند .
هنگامی که، ثابت اند، [15]اصل ITO را می تواند مورد استفاده قرار گیرد تا ثابت کند که
که دارای توزیع
جایی کهN() دارای توزیع نرمال با میانگین و واریانس است. زمانی که وابسته به زمان است:
که دارای توزیع
قیمت گذاری اوراق قرضه با استفاده از مدل هال وایت
به نظر می رسد که ارزش زمان S [16]اوراق قرضه ی تنزیلی با سررسید T یک توزیع مشخص دارد.( به ساختار [17]آفین دراینجا توجه داشته باشید!)
P(S,T)=A(S.T)exp(-B(S,T)r(S)).
جایی که
توجه داشته باشید که توزیع [18]نهایی آن ها برای P(S,T) توزیع [19]نرمال لگاریتمی است.
'قیمت گذاری اشتقاقی[20]'
با انتخاب اوراق قرضه ی [21]قابل معامله ی زمان-S (که مربوط است به [22]اندازه گیری S رو به جلو)
ما ارزش در زمان 0 که از نتیجه نهایی در زمان S مشتق شده است را به واسطه ی قضیه ی اساسی [23]قیمت گذاری آربیتراژ آزاد،داریم.
در اینجا [24]با توجه به اندازه گیری روبه جلو در نظر گرفته شده است .
علاوه بر این استدلال آربیتراژ استاندارد نشان دهنده ی قیمت آتی در زمان T برای پرداخت های زمان T با توجه به V(T)برآورد می کند
در نتیجه
در نتیجه امکان ارزش گذاری بسیاری از مشتقات وابسته به V تنها بر روی یک اوراق قرضه ی P(S,T) ،به طور تحلیلی هنگام کار روی مدل هال وایت فراهم می شود. به عنوان مثال در مورد یک اوراق قرضه قرارمی دهیم
از آنجا که P(S,T)دارای یک توزیع[25] نرمال لگاریتمی است، محاسبات جامع بکار رفته توسط [26]بلک شولز نشان می دهد که
وقتی که
و
بنابراین ارزش امروز)که قبلا درP(0,S) ضرب شده) هست:
در اینجا که انحراف استاندارد از توزیع نرمال لگاریتمی برای P(S,T) است، نشان دهنده ی مقدار نسبتا قابل توجهی از جبر است که مربوط به پارامترهای اصلی از طریق
توجه داشته باشید که مقیاس اوراق قرضه ی S بر مبنای انتظارات عموم است . در حالی که ما یک مقیاس کلی برای اصل هال وایت با روند مشخص نداریم.
که اهمیتی ندارد چون تمام آنچه که مهم است [27]نوسانات است، که[28] مستقل از واحد است.
(از آنجا که[29] سقف و کف نرخ بهره معادل [30]عرضه و تقاضای اوراق قرضه است.)
تجزیه و تحلیل بالا نشان می دهد که مدل هال وایت می تواند به طور تحلیلی سقف و کف قیمت را مشخص کند . [31]تکنیکی که جمشیدیان در رابطه با هال وایت به کار برد(به عنوان ارزش امروز از [32]سوآپشن در HW که [33]تابع یکنواخت [34]نرخ فروش است.)
بنابراین فهمیدیم که چگونه قیمت سقف برای قیمت گذاری سوآپشن کافی است.
همچنین قیمت گذاری سوآپشن به طور مستقیم در Henrard (2003) شرح داده شده است که به کار گیری مستقیم آن معمولا کارآمد تر است .
درختان و شبکه ها
با این حال، [35]ارزش نهادن به[36] ابزار ی مانند سقف قیمت و سوآپشن در درجه اول برای[37] کالیبراسیون مفید است.
استفاده ی واقعی از این مدل را می توان برای ارزش مشتقاتی که تا حدودی [38]عجیب تراند مانند سواپشن برمودا در یک شبکه و یا دیگر مشتقات در [39]زمینه ی چند ارزی مانند [40]کوانتا سواپ دائمی سررسید، به عنوان مثال در[41] بریگو وماکوریو(2001) توضیح داد.
جستار ها
[42]مدل وسیچک
[43]مدل ککس-اینگرسول- راس
[44]مدل بلک- کاروزنسیک
منابع
منابع اصلی
John Hull and Alan White, "Using Hull-White interest rate trees," Journal of Derivatives, Vol. 3, No. 3 (Spring 1996), pp 26–36
John Hull and Alan White, "Numerical procedures for implementing term structure models I," Journal of Derivatives, Fall 1994,
pp 7–16
John Hull and Alan White, "Numerical procedures for implementing term structure models II," Journal of Derivatives, Winter
1994, pp 37–48
John Hull and Alan White, "The pricing of options on interest rate caps and floors using the Hull–White model" in Advanced
Strategies in Financial Risk Management, Chapter 4, pp 59–67.
John Hull and Alan White, "One factor interest rate models and the valuation of interest rate derivative securities," Journal of
Financial and Quantitative Analysis, Vol 28, No 2, (June 1993) pp 235–254
John Hull and Alan White, "Pricing interest-rate derivative securities", The Review of Financial Studies, Vol 3, No. 4 (1990)
pp. 573–592
سایر منابع
Hull, John C. (2006). "Interest Rate Derivatives: Models of the Short Rate". Options, Futures, and Other Derivatives (6th ed.).
Upper Saddle River, N.J: Prentice Hall. pp. 657–658. ISBN 0-13-149908-4. LCCN 2005047692. OCLC 60321487.
Damiano Brigo, Fabio Mercurio (2001). Interest Rate Models — Theory and Practice with Smile, Inflation and Credit (2nd ed.
2006 ed.). Springer Verlag. ISBN 978-3-540-22149-4.
Henrard, Marc (2003). Explicit Bond Option and Swaption Formula in Heath-Jarrow-Morton One Factor Model, International
Journal of Theoretical and Applied Finance, 6(1), 57-72. Preprint SSRN (http://ssrn.com/abstract=434860).
Henrard, Marc (2009). Efficient swaptions price in Hull-White one factor model, arXiv, 0901.1776v1. Preprint arXiv
(http://arxiv.org/abs/0901.1776).
Eugen Puschkarski, Implementation of Hull-White´s No-Arbitrage Term Structure Model (http://web.archive.org/web/*
/www.angelfire.com/ny/financeinfo/Diplomnew.ppt), Diploma Thesis, Center for Central European Financial Markets
Letian Wang, Hull-White Model (http://letianwang.net/Fixed_Income/09_Hull-White_Model.htm), Fixed Income Quant Group,
DTCC (detailed numeric example and derivation)
[1] Hull–White
[2] Wikipedia
[3] bermudan swaptions
[4] John C. Hull and Alan White
[5] One-factor model
[6] short-rate model
[7] practitioners
[8]the Vasicek model
[9] the extended Vasicek model
[10] Two-factor model
[11] mean-reverting
[12] Ornstein–Uhlenbeck
[13] current term
[14] caplets and swaptions
[15] Itô's lemma
[16] discount bond
[17] affine term
[18] terminal distribution
[19] log-normally
[20] Derivative pricing
[21] numeraire
[22] switching to the S-forward measure
[23] arbitrage-free pricin
[24] is the expectation taken with respect to the forward measure
[25] lognormally distributed
[26] Black-Scholes
[27] volatility
[28] measure-independent
[29] caps/floors
[30]puts and calls
[31] trick
[32]swaption
[33]monotonic function
[34] short rate
[35] valuing
[36] vanilla instruments
[37] calibration.
[38] derivatives
[39] multi-currency context
[40] Quanto
[41]Brigo and Mercurio
[42] Vasicek model
[43] Cox–Ingersoll–Ross model
[44] Black-Karasinski model
![dr(t) = \left[\theta(t) - \alpha(t) r(t)\right]\,dt + \sigma(t)\, dW(t)\,\!](../I/m/8259749aed8399b94c56a72b7835fc37.png)
![d\,f(r(t)) = \left [\theta(t) + u - \alpha(t)\,f(r(t))\right ]dt + \sigma_1(t)\, dW_1(t)\!](../I/m/7e529b0c23c75078b540bbf462c1f4cb.png)
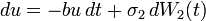

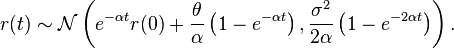
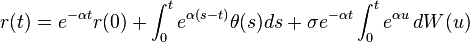
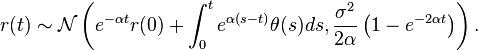
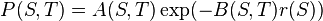
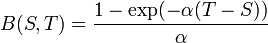
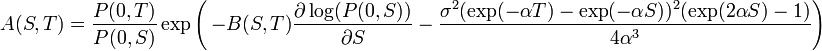
![V(t) = P(t,S)\mathbb{E}_S[V(S)| \mathcal{F}(t)].\,](../I/m/a4b64f9a8084b0b3afc8c54a50d9a7d9.png)
![F_V(t,T) = \mathbb{E}_T[V(T)|\mathcal{F}(t)].\,](../I/m/5d58f7ed4527104ed27f1eb20431f00f.png)
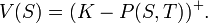
![{E}_S[(K-P(S,T))^{+}] = KN(-d_2) - F(t,S,T)N(d_1)\,](../I/m/bdd62b758f9ddab241aae227fce83520.png)