Hotelling's T-squared distribution
In statistics Hotelling's T-squared distribution is a univariate distribution proportional to the F-distribution and arises importantly as the distribution of a set of statistics which are natural generalizations of the statistics underlying Student's t-distribution. In particular, the distribution arises in multivariate statistics in undertaking tests of the differences between the (multivariate) means of different populations, where tests for univariate problems would make use of a t-test.
The distribution is named for Harold Hotelling, who developed it[1] as a generalization of Student's t-distribution.
The distribution
If the vector pd1 is Gaussian multivariate-distributed with zero mean and unit covariance matrix N(p01,pIp) and mMp is a p x p matrix with a Wishart distribution with unit scale matrix and m degrees of freedom W(pIp,m) then m(1d' pM−1pd1) has a Hotelling T2 distribution with dimensionality parameter p and m degrees of freedom.[2]
If the notation 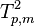 is used to denote a random variable having Hotelling's T-squared distribution with parameters p and m then, if a random variable X has Hotelling's T-squared distribution,
is used to denote a random variable having Hotelling's T-squared distribution with parameters p and m then, if a random variable X has Hotelling's T-squared distribution,
then[1]
where 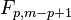 is the F-distribution with parameters p and m−p+1.
is the F-distribution with parameters p and m−p+1.
Hotelling's T-squared statistic
Hotelling's T-squared statistic is a generalization of Student's t statistic that is used in multivariate hypothesis testing, and is defined as follows.[1]
Let 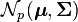 denote a p-variate normal distribution with location
denote a p-variate normal distribution with location 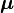 and covariance
and covariance 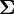 . Let
. Let
be n independent random variables, which may be represented as 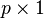 column vectors of real numbers. Define
column vectors of real numbers. Define
to be the sample mean. It can be shown that
where 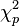 is the chi-squared distribution with p degrees of freedom. To show this use the fact that
is the chi-squared distribution with p degrees of freedom. To show this use the fact that 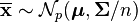 and then derive the characteristic function of the random variable
and then derive the characteristic function of the random variable 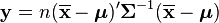 . This is done below,
. This is done below,
However, 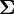 is often unknown and we wish to do hypothesis testing on the location
is often unknown and we wish to do hypothesis testing on the location 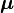 .
.
Sum of p squared t's
Define
to be the sample covariance. Here we denote transpose by an apostrophe. It can be shown that 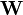 is a positive (semi) definite matrix and
is a positive (semi) definite matrix and 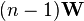 follows a p-variate Wishart distribution with n−1 degrees of freedom.[3] Hotelling's T-squared statistic is then defined[4] to be
follows a p-variate Wishart distribution with n−1 degrees of freedom.[3] Hotelling's T-squared statistic is then defined[4] to be
and, also from above,
i.e.
where 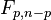 is the F-distribution with parameters p and n−p. In order to calculate a p value, multiply the t2 statistic by the above constant and use the F-distribution.
is the F-distribution with parameters p and n−p. In order to calculate a p value, multiply the t2 statistic by the above constant and use the F-distribution.
Hotelling's two-sample T-squared statistic
If 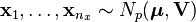 and
and 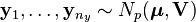 , with the samples independently drawn from two independent multivariate normal distributions with the same mean and covariance, and we define
, with the samples independently drawn from two independent multivariate normal distributions with the same mean and covariance, and we define
as the sample means, and
as the unbiased pooled covariance matrix estimate, then Hotelling's two-sample T-squared statistic is
and it can be related to the F-distribution by[3]
The non-null distribution of this statistic is the noncentral F-distribution (the ratio of a non-central Chi-squared random variable and an independent central Chi-squared random variable)
with
where  is the difference vector between the population means.
is the difference vector between the population means.
More robust and powerful tests than Hotelling's two-sample test have been proposed in the literature, see for example the interpoint distance based tests which can be applied also when the number of variables is comparable with, or even larger than, the number of subjects.[5][6]
In the two variable case, the formula simplifies nicely allowing appreciation of how the correlation,  ,
between the variables affects
,
between the variables affects 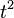 . If we define
. If we define
and
then
Thus, if the differences in the two rows of the vector 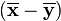 are of the same sign, in general,
are of the same sign, in general, 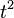 becomes smaller as
becomes smaller as  becomes more positive. If the differences are of opposite sign
becomes more positive. If the differences are of opposite sign 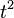 becomes larger as
becomes larger as  becomes more positive.
becomes more positive.
See also
- Student's t-test in univariate statistics
- Student's t-distribution in univariate probability theory
- Multivariate Student distribution.
- F-distribution (commonly tabulated or available in software libraries, and hence used for testing the T-squared statistic using the relationship given above)
- Wilks' lambda distribution (in multivariate statistics Wilks's Λ is to Hotelling's T2 as Snedecor's F is to Student's t in univariate statistics).
References
- 1 2 3 Hotelling, H. (1931). "The generalization of Student's ratio". Annals of Mathematical Statistics 2 (3): 360–378. doi:10.1214/aoms/1177732979.
- ↑ Eric W. Weisstein, CRC Concise Encyclopedia of Mathematics, Second Edition, Chapman & Hall/CRC, 2003, p. 1408
- 1 2 Mardia, K. V.; Kent, J. T.; Bibby, J. M. (1979). Multivariate Analysis. Academic Press. ISBN 0-12-471250-9.
- ↑ http://www.itl.nist.gov/div898/handbook/pmc/section5/pmc543.htm
- ↑ Marozzi, M. (2014). "Multivariate tests based on interpoint distances with application to magnetic resonance imaging". Statistical Methods in Medical Research. doi:10.1177/0962280214529104.
- ↑ Marozzi, M. (2015). "Multivariate multidistance tests for high-dimensional low sample size case-control studies". Statistics in Medicine 34. doi:10.1002/sim.6418.
External links
- Prokhorov, A.V. (2001), "Hotelling T2-distribution", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
| ||||||||||||||
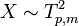
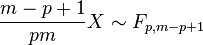
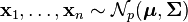
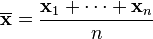
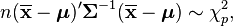
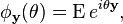
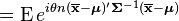
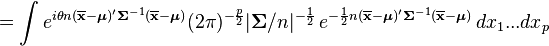
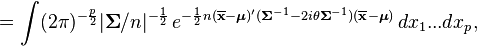
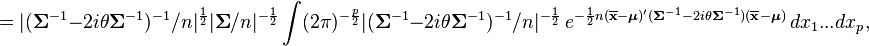
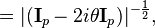
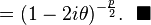
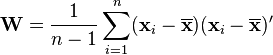
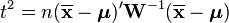
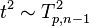
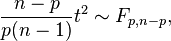
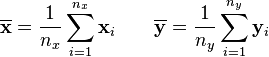
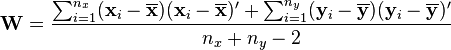
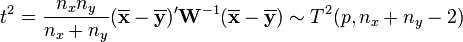
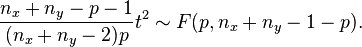
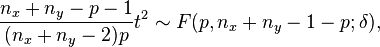
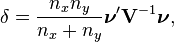


![t^2 = \frac{n_x n_y}{(n_x+n_y)(1-r^2)} \left [ \left ( \frac{d_1}{SD_1} \right )^2+\left ( \frac{d_2}{SD_2} \right )^2-2r \left ( \frac{d_1}{SD_1} \right )\left ( \frac{d_2}{SD_2} \right ) \right ]](../I/m/d8f754bcef7a7c7cc00baf1c01ed51ac.png)