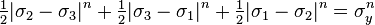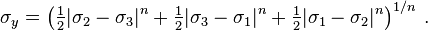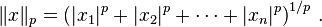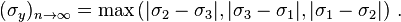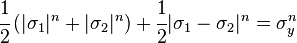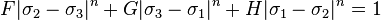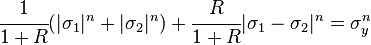Hosford yield criterion

The Hosford yield criterion is a function that is used to determine whether a material has undergone plastic yielding under the action of stress.

Hosford yield criterion for isotropic plasticity

The plane stress, isotropic, Hosford yield surface for three values of n

The Hosford yield criterion for isotropic materials ^[1] is a generalization of the von Mises yield criterion. It has the form

\tfrac{1}{2}|\sigma_2-\sigma_3|^n + \tfrac{1}{2}|\sigma_3-\sigma_1|^n + \tfrac{1}{2}|\sigma_1-\sigma_2|^n = \sigma_y^n \,

where $\sigma_i$ , i=1,2,3 are the principal stresses, $n$ is a material-dependent exponent and $\sigma_y$ is the yield stress in uniaxial tension/compression.

Alternatively, the yield criterion may be written as

\sigma_y = \left(\tfrac{1}{2}|\sigma_2-\sigma_3|^n + \tfrac{1}{2}|\sigma_3-\sigma_1|^n + \tfrac{1}{2}|\sigma_1-\sigma_2|^n\right)^{1/n} \,.

This expression has the form of an L^p norm which is defined as

\ \|x\|_p=\left(|x_1|^p+|x_2|^p+\cdots+|x_n|^p\right)^{1/p} \,.

When $p = \infty$ , the we get the L^∞ norm,

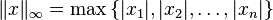\ \|x\|_\infty=\max \left\{|x_1|, |x_2|, \ldots, |x_n|\right\}

. Comparing this with the Hosford criterion

indicates that if n = ∞, we have

(\sigma_y)_{n\rightarrow\infty} = \max \left(|\sigma_2-\sigma_3|, |\sigma_3-\sigma_1|,|\sigma_1-\sigma_2|\right) \,.

This is identical to the Tresca yield criterion.

Therefore, when n = 1 or n goes to infinity the Hosford criterion reduces to the Tresca yield criterion. When n = 2 the Hosford criterion reduces to the von Mises yield criterion.

Note that the exponent n does not need to be an integer.

Hosford yield criterion for plane stress

For the practically important situation of plane stress, the Hosford yield criterion takes the form

\cfrac{1}{2}\left(|\sigma_1|^n + |\sigma_2|^n\right) + \cfrac{1}{2}|\sigma_1-\sigma_2|^n = \sigma_y^n \,

A plot of the yield locus in plane stress for various values of the exponent $n \ge 1$ is shown in the adjacent figure.

Logan-Hosford yield criterion for anisotropic plasticity

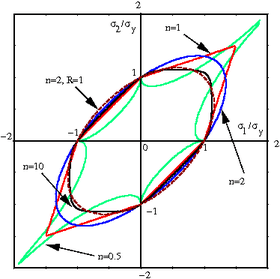
The plane stress, anisotropic, Hosford yield surface for four values of n and R=2.0

The Logan-Hosford yield criterion for anisotropic plasticity ^[2]^[3] is similar to Hill's generalized yield criterion and has the form

F|\sigma_2-\sigma_3|^n + G|\sigma_3-\sigma_1|^n + H|\sigma_1-\sigma_2|^n = 1 \,

where F,G,H are constants, $\sigma_i$ are the principal stresses, and the exponent n depends on the type of crystal (bcc, fcc, hcp, etc.) and has a value much greater than 2.^[4] Accepted values of $n$ are 6 for bcc materials and 8 for fcc materials.

Though the form is similar to Hill's generalized yield criterion, the exponent n is independent of the R-value unlike the Hill's criterion.

Logan-Hosford criterion in plane stress

Under plane stress conditions, the Logan-Hosford criterion can be expressed as

\cfrac{1}{1+R} (|\sigma_1|^n + |\sigma_2|^n) + \cfrac{R}{1+R} |\sigma_1-\sigma_2|^n = \sigma_y^n

where $R$ is the R-value and $\sigma_y$ is the yield stress in uniaxial tension/compression. For a derivation of this relation see Hill's yield criteria for plane stress. A plot of the yield locus for the anisotropic Hosford criterion is shown in the adjacent figure. For values of $n$ that are less than 2, the yield locus exhibits corners and such values are not recommended.^[4]

References

↑ Hosford, W. F. (1972). A generalized isotropic yield criterion, Journal of Applied Mechanics, v. 39, n. 2, pp. 607-609.
↑ Hosford, W. F., (1979), On yield loci of anisotropic cubic metals, Proc. 7th North American Metalworking Conf., SME, Dearborn, MI.
↑ Logan, R. W. and Hosford, W. F., (1980), Upper-Bound Anisotropic Yield Locus Calculations Assuming< 111>-Pencil Glide, International Journal of Mechanical Sciences, v. 22, n. 7, pp. 419-430.
1 2 Hosford, W. F., (2005), Mechanical Behavior of Materials, p. 92, Cambridge University Press.