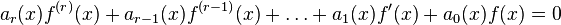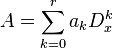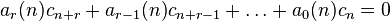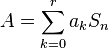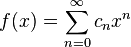Holonomic function
In mathematics, a holonomic function is a smooth function in several variables that is a solution of a system of linear homogeneous differential equations with polynomial coefficients and satisfies a suitable dimension condition in terms of D-modules theory. More precisely, a holonomic function is an element of a holonomic module of smooth functions. Holonomic functions can also be described as differentiably finite functions, also known as D-finite functions. When a power series in the variables is the Taylor expansion of a holonomic function, the sequence of its coefficients, in one or several indices, is also called holonomic. Holonomic sequences are also called P-recursive sequences: they are defined recursively by multivariate recurrences satisfied by the whole sequence and by suitable specializations of it. The situation simplifies in the univariate case: any univariate sequence that satisfies a linear homogeneous recurrence relation with polynomial coefficients, or equivalently a linear homogeneous difference equation with polynomial coefficients, is holonomic.[1][2]
Holonomic functions and sequences in one variable
Let  be a field of characteristic 0 (for example,
be a field of characteristic 0 (for example, 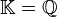 or
or 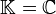 ).
).
A function 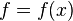 is called D-finite (or holonomic) if there exist polynomials
is called D-finite (or holonomic) if there exist polynomials ![a_r(x), a_{r-1}(x), \ldots, a_0(x) \in \mathbb{K}[x]](../I/m/96f96ea893c92cb13f34666a8a19d759.png) such that
such that
holds for all x. This can also be written as 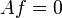 where
where
and  is the differential operator that maps
is the differential operator that maps 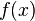 to
to  .
.  is called an annihilating operator of f (the annihilating operators of
is called an annihilating operator of f (the annihilating operators of  form an ideal in the ring
form an ideal in the ring ![\mathbb{K}[x][D_x]](../I/m/327e5180d33ea36ec8a8b4187b23028f.png) , called the annihilator of
, called the annihilator of  ). The quantity r is called the order of the annihilating operator (by extension, the sequence c is said to have order r when an annihilating operator of such order exists).
). The quantity r is called the order of the annihilating operator (by extension, the sequence c is said to have order r when an annihilating operator of such order exists).
A sequence 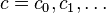 is called P-recursive (or holonomic) if there exist polynomials
is called P-recursive (or holonomic) if there exist polynomials ![a_r(n), a_{r-1}(n), \ldots, a_0(n) \in \mathbb{K}[n]](../I/m/c292d0c81255296d4f64f1b0e064a7cd.png) such that
such that
holds for all n. This can also be written as 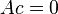 where
where
and  the shift operator that maps
the shift operator that maps 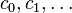 to
to 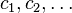 .
.  is called an annihilating operator of c (the annihilating operators of
is called an annihilating operator of c (the annihilating operators of  form an ideal in the ring
form an ideal in the ring ![\mathbb{K}[n][S_n]](../I/m/c88ace93e20807a9adc985a3d2c6ca15.png) , called the annihilator of
, called the annihilator of  ). The quantity r is called the order of the annihilating operator (by extension, the sequence c is said to have order r when an annihilating operator of such order exists).
). The quantity r is called the order of the annihilating operator (by extension, the sequence c is said to have order r when an annihilating operator of such order exists).
Holonomic functions are precisely the generating functions of holonomic sequences: if 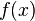 is holonomic, then the coefficients
is holonomic, then the coefficients  in the power series expansion
in the power series expansion
form a holonomic sequence. Conversely, for a given holonomic sequence  , the function defined by the above sum is holonomic (this is true in the sense of formal power series, even if the sum has a zero radius of convergence).
, the function defined by the above sum is holonomic (this is true in the sense of formal power series, even if the sum has a zero radius of convergence).
Closure properties
Holonomic functions (or sequences) satisfy several closure properties. In particular, holonomic functions (or sequences) form a ring. They are not closed under division, however, and therefore do not form a field.
If 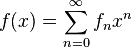 and
and 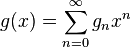 are holonomic functions, then the following functions are also holonomic:
are holonomic functions, then the following functions are also holonomic:
-
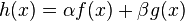 , where
, where  and
and  are constants
are constants -
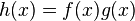 (the Cauchy product of the sequences)
(the Cauchy product of the sequences) -
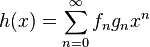 (the Hadamard product of the sequences)
(the Hadamard product of the sequences) -
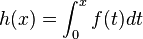
-
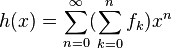
-
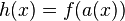 , where
, where  is any algebraic function. However,
is any algebraic function. However, 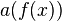 is not generally holonomic.
is not generally holonomic.
A crucial property of holonomic functions is that the closure properties are effective: given annihilating operators for  and
and  , an annihilating operator for
, an annihilating operator for  as defined using any of the above operations can be computed explicitly.
as defined using any of the above operations can be computed explicitly.
Examples of holonomic functions
Examples of holonomic functions include all algebraic functions and some transcendental functions, such as 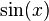 ,
, 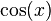 ,
,  , and
, and 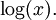 [3] More generally, the generalized hypergeometric function
[3] More generally, the generalized hypergeometric function 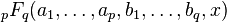 is holonomic, considered as a function of
is holonomic, considered as a function of  with all the parameters
with all the parameters  ,
, 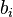 held fixed. As a consequence, the following special functions are all holonomic with respect to
held fixed. As a consequence, the following special functions are all holonomic with respect to  :
:
- The error function
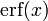
- The Bessel functions
 ,
, 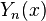 ,
, 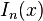 ,
, 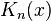
- The Airy functions
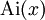 ,
, 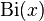
- The classical orthogonal polynomials (including Legendre polynomials
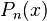 , Chebyshev polynomials
, Chebyshev polynomials  and
and 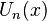 , etc.)
, etc.)
The class of holonomic functions is a strict superset of the class of hypergeometric functions. Examples of special functions that are holonomic but not hypergeometric include the Heun functions.
Examples of holonomic sequences include:
- The sequence of Fibonacci numbers

- The sequence of factorials

- The binomial coefficients
 (as functions of either n or k)
(as functions of either n or k) - The harmonic numbers
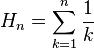 , or more generally
, or more generally 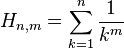 for any integer m
for any integer m - The Motzkin numbers
Examples of non-holonomic functions
- The function
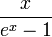 is not holonomic, and therefore the Bernoulli numbers are not a holonomic sequence. This follows from the fact that the function has infinitely many singularities, and therefore cannot satisfy a linear differential equation with polynomial coefficients, which necessarily has only finitely many singular points. More generally, the quotient of two holonomic functions is not necessarily holonomic (but can be, in special cases).
is not holonomic, and therefore the Bernoulli numbers are not a holonomic sequence. This follows from the fact that the function has infinitely many singularities, and therefore cannot satisfy a linear differential equation with polynomial coefficients, which necessarily has only finitely many singular points. More generally, the quotient of two holonomic functions is not necessarily holonomic (but can be, in special cases). - The function tan(x)+sec(x) is not holonomic, and therefore the number of alternating permutations are not a holonomic sequence.[4]
- The number of integer partitions p(n) is not holonomic (ibid.)
- The sequence
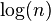 , the sequence
, the sequence 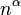 where
where 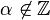 , and the sequence of prime numbers are not holonomic (ibid.)
, and the sequence of prime numbers are not holonomic (ibid.) - The number irreducible and connected permutations.[5]
Algorithms and software
Holonomic functions are a powerful tool in computer algebra. A holonomic function or sequence can be represented by a finite amount of data, namely an annihilating operator and a finite set of initial values, and the closure properties allow carrying out operations such as equality testing, summation and integration in an algorithmic fashion. In recent years, these techniques have allowed giving automated proofs of a large number of special function and combinatorial identities.
Moreover, there exist fast algorithms for evaluating holonomic functions to arbitrary precision at any point in the complex plane, and for numerically computing any entry in a holonomic sequence.
Software for working with holonomic functions includes:
- The HolonomicFunctions package for Mathematica, developed by Christoph Koutschan, which supports computing closure properties and proving identities for univariate and multivariate holonomic functions
- The algolib library for Maple, which includes the following packages:
References
- ↑ Zeilberger, Doron (1990). "A holonomic systems approach to special functions identities". Journal of Computational and Applied Mathematics 32 (3): 321–368. doi:10.1016/0377-0427(90)90042-X. ISSN 0377-0427. MR 1090884.
- ↑ Kauers, Manuel; Paule, Peter (2011). The Concrete Tetrahedron: Symbolic Sums, Recurrence Equations, Generating Functions, Asymptotic Estimates. Text and Monographs in Symbolic Computation. New York: Springer. ISBN 978-3-7091-0444-6.
- ↑ Mallinger, Christian (1996). Algorithmic Manipulations and Transformations of Univariate Holonomic Functions and Sequences (PDF) (Thesis). p. 3. Retrieved 4 June 2013.
- ↑ Flajolet, Philippe; Gerhold, Stefan; Salvy, Bruno (2005), On the non-holonomic character of logarithms, powers, and the n-th prime function
- ↑ Martin Klazar, Irreducible and connected permutations, ITI Series preprint no. 122 (2003), 24 pp.
Further reading
- Flajolet, Philippe; Sedgewick, Robert. Analytic Combinatorics. Cambridge University Press. ISBN 0521898064.
- Stanley, Richard P. (1999). Enumerative Combinatorics, Volume 2. Cambridge University Press. ISBN 0-521-56069-1.