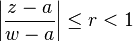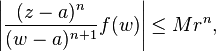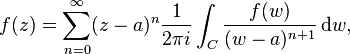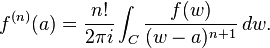Analyticity of holomorphic functions
In complex analysis a complex-valued function ƒ of a complex variable z:
- is said to be holomorphic at a point a if it is differentiable at every point within some open disk centered at a, and
- is said to be analytic at a if in some open disk centered at a it can be expanded as a convergent power series
- (this implies that the radius of convergence is positive).
One of the most important theorems of complex analysis is that holomorphic functions are analytic. Among the corollaries of this theorem are
- the identity theorem that two holomorphic functions that agree at every point of an infinite set S with an accumulation point inside the intersection of their domains also agree everywhere in every connected open subset of their domains that contains the set S, and
- the fact that, since power series are infinitely differentiable, so are holomorphic functions (this is in contrast to the case of real differentiable functions), and
- the fact that the radius of convergence is always the distance from the center a to the nearest singularity; if there are no singularities (i.e., if ƒ is an entire function), then the radius of convergence is infinite. Strictly speaking, this is not a corollary of the theorem but rather a by-product of the proof.
- no bump function on the complex plane can be entire. In particular, on any connected open subset of the complex plane, there can be no bump function defined on that set which is holomorphic on the set. This has important ramifications for the study of complex manifolds, as it precludes the use of partitions of unity. In contrast the partition of unity is a tool which can be used on any real manifold.
Proof
The argument, first given by Cauchy, hinges on Cauchy's integral formula and the power series development of the expression
Let D be an open disk centered at a and suppose ƒ is differentiable everywhere within an open neighborhood containing the closure of D. Let C be the positively oriented (i.e., counterclockwise) circle which is the boundary of D and z a point in D. Starting with Cauchy's integral formula, we have
Interchange of the integral and infinite sum is justified by observing that 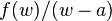 is bounded on C by some positive number M, while for all w in C
is bounded on C by some positive number M, while for all w in C
for some positive r as well. We therefore have
on C, and as the Weierstrass M-test shows the series converges uniformly, the sum and the integral may be interchanged.
As the factor (z − a)n does not depend on the variable of integration w, it may be factored out to yield
which has the desired form of a power series in z:
with coefficients
Remarks
- Since power series can be differentiated term-wise, applying the above argument in the reverse direction and the power series expression for
- gives
- This is a Cauchy integral formula for derivatives. Therefore the power series obtained above is the Taylor series of ƒ.
- The argument works if z is any point that is closer to the center a than is any singularity of ƒ. Therefore the radius of convergence of the Taylor series cannot be smaller than the distance from a to the nearest singularity (nor can it be larger, since power series have no singularities in the interiors of their circles of convergence).
- A special case of the identity theorem follows from the preceding remark. If two holomorphic functions agree on a (possibly quite small) open neighborhood U of a, then they coincide on the open disk Bd(a), where d is the distance from a to the nearest singularity.
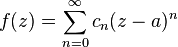
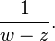
![\begin{align}f(z) &{}= {1 \over 2\pi i}\int_C {f(w) \over w-z}\,\mathrm{d}w \\[10pt]
&{}= {1 \over 2\pi i}\int_C {f(w) \over (w-a)-(z-a)} \,\mathrm{d}w \\[10pt]
&{}={1 \over 2\pi i}\int_C {1 \over w-a}\cdot{1 \over 1-{z-a \over w-a}}f(w)\,\mathrm{d}w \\[10pt]
&{}={1 \over 2\pi i}\int_C {1 \over w-a}\cdot{\sum_{n=0}^\infty\left({z-a \over w-a}\right)^n} f(w)\,\mathrm{d}w \\[10pt]
&{}=\sum_{n=0}^\infty{1 \over 2\pi i}\int_C {(z-a)^n \over (w-a)^{n+1}} f(w)\,\mathrm{d}w.\end{align}](../I/m/08024f8fc30b43e95a571874c73d9406.png)