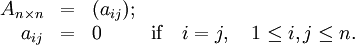Hollow matrix

In mathematics, a hollow matrix may refer to one of several related classes of matrix.

Sparse

A hollow matrix may be one with "few" non-zero entries: that is, a sparse matrix.^[1]

Diagonal entries all zero

A hollow matrix may be a square matrix whose diagonal elements are all equal to zero .^[2] The most obvious example is the real skew-symmetric matrix. Other examples are the adjacency matrix of a finite simple graph; a distance matrix or Euclidean distance matrix.

If A is an n×n hollow matrix, then the elements of A are given by

\begin{array}{rlll} A_{n\times n} & = & (a_{ij}); \\ a_{ij} & = & 0 & \mbox{if} \quad i=j,\quad 1\le i,j \le n.\, \end{array}

In other words, any square matrix which takes the form $\left(\begin{array}{ccccc} 0\\ & 0\\ & & \ddots\\ & & & 0\\ & & & & 0\end{array}\right)$ is a hollow matrix.

For example: $\left(\begin{array}{ccccc} 0 & 2 & 6 & \frac{1}{3} & 4\\2 & 0 & 4 & 8 & 0\\ 9 & 4 & 0 & 2 & 933\\ 1 & 4 & 4 & 0 & 6\\ 7 & 9 & 23 & 8 & 0\end{array}\right)$ is an example of a hollow matrix.

Properties

The trace of A is trivially zero.

The linear map represented by A (with respect to a fixed basis) maps each basis vector e onto the image of the complement of <e>.

Gershgorin's Circle Theorem shows that the moduli of the eigenvalues of A are equal to the sum of the moduli of the non-diagonal row entries.

Block of zeroes

A hollow matrix may be a square n×n matrix with an r×s block of zeroes where r+s>n.^[3]

References

↑ Pierre Massé (1962). Optimal Investment Decisions: Rules for Action and Criteria for Choice. Prentice-Hall. p. 142.
↑ James E. Gentle (2007). Matrix Algebra: Theory, Computations, and Applications in Statistics. Springer-Verlag. p. 42. ISBN 0-387-70872-3.
↑ Paul Cohn (2006). Free Ideal Rings and Localization in General Rings. Cambridge University Press. p. 430. ISBN 0-521-85337-0.

This article is issued from Wikipedia - version of the Thursday, May 14, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.