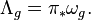Hodge bundle

In mathematics, the Hodge bundle, named after W. V. D. Hodge, appears in the study of families of curves, where it provides an invariant in the moduli theory of algebraic curves. Furthermore, it has applications to the theory of modular forms on reductive algebraic groups^[1] and string theory.^[2]

Definitions

Let 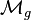$\mathcal{M}_g$ be the moduli space of algebraic curves of genus g curves over some scheme. The Hodge bundle Λ_g is a vector bundle on 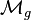$\mathcal{M}_g$ whose fiber at a point C in 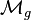$\mathcal{M}_g$ is the space of holomorphic differentials on the curve C. To define the Hodge bundle, let 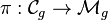$\pi:\mathcal{C}_g\rightarrow\mathcal{M}_g$ be the universal algebraic curve of genus g and let ω_g be its relative dualizing sheaf. The Hodge bundle is the pushforward of this sheaf, i.e.^[3]

\Lambda_g=\pi_*\omega_g.\,

Notes

References

van der Geer, Gerard (2008), "Siegel modular forms and their applications", in Ranestad, Kristian, The 1-2-3 of modular forms, Universitext, Berlin: Springer-Verlag, pp. 181–245, doi:10.1007/978-3-540-74119-0, ISBN 978-3-540-74117-6, MR 2409679
Harris, Joe; Morrison, Ian (1998), Moduli of curves, Graduate Texts in Mathematics 187, Springer-Verlag, ISBN 978-0-387-98429-2, MR 1631825
Liu, Kefeng (2006), "Localization and conjectures from string duality", in Ge, Mo-Lin; Zhang, Weiping, Differential geometry and physics, Nankai Tracts in Mathematics 10, World Scientific, pp. 63–105, ISBN 978-981-270-377-4, MR 2322389

Topics in algebraic curves

Rational curves

Elliptic curves

Analytic theory	Elliptic function Elliptic integral Fundamental pair of periods Modular form

Arithmetic theory	Counting points on elliptic curves Division polynomials Hasse's theorem on elliptic curves Mazur's torsion theorem Modular elliptic curve Modularity theorem Mordell–Weil theorem Nagell–Lutz theorem Supersingular elliptic curve Schoof's algorithm Schoof–Elkies–Atkin algorithm

Applications	Elliptic curve cryptography Elliptic curve primality

Higher genus

Plane curves

Riemann surfaces

Constructions

Structure of curves

Divisors on curves	Abel–Jacobi map Brill–Noether theory Clifford's theorem on special divisors Gonality of an algebraic curve Jacobian variety Riemann–Roch theorem Weierstrass point Weil reciprocity law

Moduli	ELSV formula Gromov–Witten invariant Hodge bundle Moduli of algebraic curves Stable curve

Morphisms	Hasse–Witt matrix Riemann–Hurwitz formula Prym variety Weber's theorem

Singularities	Acnode Crunode Cusp Delta invariant Tacnode

Vector bundles	Birkhoff–Grothendieck theorem Stable vector bundle Vector bundles on algebraic curves

This article is issued from Wikipedia - version of the Tuesday, August 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Hodge bundle

Definitions

See also

Notes

References