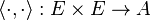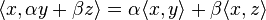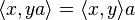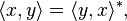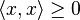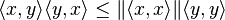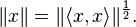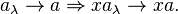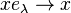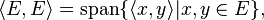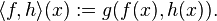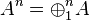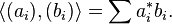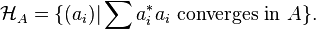Hilbert C*-module

Hilbert C*-modules are mathematical objects which generalise the notion of a Hilbert space (which itself is a generalisation of Euclidean space), in that they endow a linear space with an "inner product" which takes values in a C*-algebra. Hilbert C*-modules were first introduced in the work of Irving Kaplansky in 1953, which developed the theory for commutative, unital algebras (though Kaplansky observed that the assumption of a unit element was not "vital").[1] In the 1970s the theory was extended to non-commutative C*-algebras independently by William Lindall Paschke[2] and Marc Rieffel, the latter in a paper which used Hilbert C*-modules to construct a theory of induced representations of C*-algebras.[3] Hilbert C*-modules are crucial to Kasparov's formulation of KK-theory,[4] and provide the right framework to extend the notion of Morita equivalence to C*-algebras.[5] They can be viewed as the generalization of vector bundles to noncommutative C*-algebras and as such play an important role in noncommutative geometry, notably in C*-algebraic quantum group theory,[6][7] and groupoid C*-algebras.

Definitions

Inner-product A-modules

Let A be a C*-algebra (not assumed to be commutative or unital), its involution denoted by *. An inner-product A-module (or pre-Hilbert A-module) is a complex linear space E which is equipped with a compatible right A-module structure, together with a map

\langle \cdot, \cdot \rangle : E \times E \rightarrow A

which satisfies the following properties:

\langle x, \alpha y + \beta z \rangle = \alpha \langle x, y \rangle + \beta \langle x, z \rangle
(i.e. the inner product is linear in its second argument).
\langle x, ya \rangle = \langle x, y \rangle a
\langle x, y \rangle = \langle y, x \rangle^*,
from which it follows that the inner product is conjugate linear in its first argument (i.e. it is a sesquilinear form).
\langle x, x \rangle \geq 0
and
\langle x, x \rangle = 0 \iff x = 0.
(An element of a C*-algebra A is said to be positive if it is self-adjoint with non-negative spectrum.)[8][9]

Hilbert A-modules

An analogue to the Cauchy-Schwarz inequality holds for an inner-product A-module E:[10]

\langle x, y \rangle \langle y, x \rangle \leq \Vert \langle x, x \rangle \Vert \langle y, y \rangle

for x, y in E.

On the pre-Hilbert module E, define a norm by

\Vert x \Vert = \Vert \langle x, x \rangle \Vert^\frac{1}{2}.

The norm-completion of E, still denoted by E, is said to be a Hilbert A-module or a Hilbert C*-module over the C*-algebra A. The Cauchy-Schwarz inequality implies the inner product is jointly continuous in norm and can therefore be extended to the completion.

The action of A on E is continuous: for all x in E

a_{\lambda} \rightarrow a \Rightarrow xa_{\lambda} \rightarrow xa.

Similarly, if {eλ} is an approximate unit for A (a net of self-adjoint elements of A for which aeλ and eλa tend to a for each a in A), then for x in E

xe_\lambda \rightarrow x

whence it follows that EA is dense in E, and x1 = x when A is unital.

Let

\langle E, E \rangle = \operatorname{span} \{ \langle x, y \rangle | x, y \in E \},

then the closure of <E,E> is a two-sided ideal in A. Two-sided ideals are C*-subalgebras and therefore possess approximate units. One can verify that E<E,E> is dense in E. In the case when <E,E> is dense in A, E is said to be full. This does not generally hold.

Examples

Hilbert spaces

A complex Hilbert space H is a Hilbert C-module under its inner product, the complex numbers being a C*-algebra with an involution given by complex conjugation.

Vector bundles

If X is a locally compact Hausdorff space and E a vector bundle over X with a Riemannian metric g, then the space of continuous sections of E is a Hilbert C(X)-module. The inner product is given by

\langle f,h\rangle (x):=g(f(x),h(x)).

The converse holds as well: Every countably generated Hilbert C*-module over a commutative C*-algebra A = C(X) is isomorphic to the space of sections vanishing at infinity of a continuous field of Hilbert spaces over X.

C*-algebras

Any C*-algebra A is a Hilbert A-module under the inner product <a,b> = a*b. By the C*-identity, the Hilbert module norm coincides with C*-norm on A.

The (algebraic) direct sum of n copies of A

A^n = \oplus_1^n A

can be made into a Hilbert A-module by defining

\langle (a_i), (b_i) \rangle = \sum a_i^* b_i.

One may also consider the following subspace of elements in the countable direct product of A

\mathcal{H}_A = \{ (a_i) | \sum a_i^{*}a_i\text{ converges in }A \}.

Endowed with the obvious inner product (analogous to that of An), the resulting Hilbert A-module is called the standard Hilbert module.

See also

Notes

  1. ↑ Kaplansky, I. (1953). "Modules over operator algebras". American Journal of Mathematics 75 (4): 839–853. doi:10.2307/2372552. JSTOR 2372552.
  2. ↑ Paschke, W. L. (1973). "Inner product modules over B*-algebras". Transactions of the American Mathematical Society 182: 443–468. doi:10.2307/1996542. JSTOR 1996542.
  3. ↑ Rieffel, M. A. (1974). "Induced representations of C*-algebras". Advances in Mathematics (Elsevier) 13 (2): 176–257. doi:10.1016/0001-8708(74)90068-1.
  4. ↑ Kasparov, G. G. (1980). "Hilbert C*-modules: Theorems of Stinespring and Voiculescu". Journal of Operator Theory (Theta Foundation) 4: 133–150.
  5. ↑ Rieffel, M. A. (1982). "Morita equivalence for operator algebras". Proceedings of Symposia in Pure Mathematics (American Mathematical Society) 38: 176–257.
  6. ↑ Baaj, S.; Skandalis, G. (1993). "Unitaires multiplicatifs et dualité pour les produits croisés de C*-algèbres". Annales Scientifiques de l'École Normale Supérieure 26 (4): 425–488.
  7. ↑ Woronowicz, S. L. (1991). "Unbounded elements affiliated with C*-algebras and non-compact quantum groups". Communications in Mathematical Physics 136 (2): 399–432. Bibcode:1991CMaPh.136..399W. doi:10.1007/BF02100032.
  8. ↑ Arveson, William (1976). An Invitation to C*-Algebras. Springer-Verlag. p. 35.
  9. ↑ In the case when A is non-unital, the spectrum of an element is calculated in the C*-algebra generated by adjoining a unit to A.
  10. ↑ This result in fact holds for semi-inner-product A-modules, which may have non-zero elements x such that <x,x> = 0, as the proof does not rely on the nondegeneracy property.

References

External links

This article is issued from Wikipedia - version of the Wednesday, September 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.