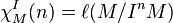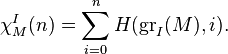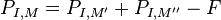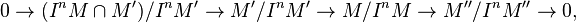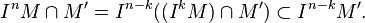Hilbert–Samuel function

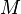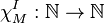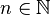In commutative algebra the Hilbert–Samuel function, named after David Hilbert and Pierre Samuel,[1] of a nonzero finitely generated module M over a commutative Noetherian local ring A and a primary ideal I of A is the map \chi_{M}^{I}:\mathbb{N}\rightarrow\mathbb{N} such that, for all n\in\mathbb{N},

\chi_{M}^{I}(n)=\ell(M/I^{n}M)

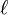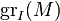where \ell denotes the length over A. It is related to the Hilbert function of the associated graded module \operatorname{gr}_I(M) by the identity

\chi_M^I (n)=\sum_{i=0}^n H(\operatorname{gr}_I(M),i).

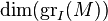For sufficiently large n, it coincides with a polynomial function of degree equal to \dim(\operatorname{gr}_I(M)).[2]

Examples

For the ring of formal power series in two variables k[[x,y]] taken as a module over itself and graded by the order and the ideal generated by the monomials x2 and y3 we have

\chi(1)=1,\quad \chi(2)=3,\quad \chi(3)=5,\quad \chi(4)=6\text{ and } \chi(k)=6\text{ for }k > 4.[2]

Degree bounds

Unlike the Hilbert function, the Hilbert–Samuel function is not additive on an exact sequence. However, it is still reasonably close to being additive, as a consequence of the Artin–Rees lemma. We denote by P_{I, M} the Hilbert-Samuel polynomial; i.e., it coincides with the Hilbert–Samuel function for large integers.

Theorem — Let 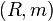(R, m) be a Noethrian local ring and I an m-primary ideal. If

0 \to M' \to M \to M'' \to 0

is an exact sequence of finitely generated R-modules and if 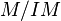M/I M has finite length,[3] then we have:[4]

P_{I, M} = P_{I, M'} + P_{I, M''} - F

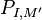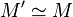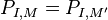where F is a polynomial of degree strictly less than that of P_{I, M'} and having positive leading coefficient. In particular, if M' \simeq M, then the degree of P_{I, M''} is strictly less than that of P_{I, M} = P_{I, M'}.

Proof: Tensoring the given exact sequence with 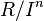R/I^n and computing the kernel we get the exact sequence:

0 \to (I^n M \cap M')/I^n M' \to M'/I^n M' \to M/I^n M \to M''/I^n M'' \to 0,

which gives us:

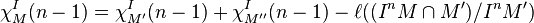\chi_M^I(n-1) = \chi_{M'}^I(n-1) + \chi_{M''}^I(n-1) - \ell((I^n M \cap M')/I^n M').

The third term on the right can be estimated by Artin-Rees. Indeed, by the lemma, for large n and some k,

I^n M \cap M' = I^{n-k} ((I^k M) \cap M') \subset I^{n-k} M'.

Thus,

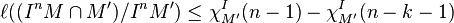\ell((I^n M \cap M') / I^n M') \le \chi^I_{M'}(n-1) - \chi^I_{M'}(n-k-1).

This gives the desired degree bound.

See also

References

  1. ↑ H. Hironaka, Resolution of Singularities of an Algebraic Variety Over a Field of Characteristic Zero: I. Ann. of Math. 2nd Ser., Vol. 79, No. 1. (Jan., 1964), pp. 109-203.
  2. ↑ 2.0 2.1 Atiyah, M. F. and MacDonald, I. G. Introduction to Commutative Algebra. Reading, MA: Addison–Wesley, 1969.
  3. ↑ This implies that 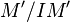M'/IM' and M''/IM'' also have finite length.
  4. ↑ Eisenbud, David, Commutative Algebra with a View Toward Algebraic Geometry, Graduate Texts in Mathematics, 150, Springer-Verlag, 1995, ISBN 0-387-94268-8. Lemma 12.3.
This article is issued from Wikipedia - version of the Friday, May 15, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.