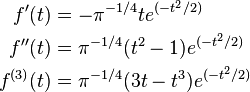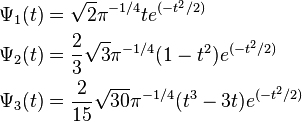Hermitian wavelet

Hermitian wavelets are a family of continuous wavelets, used in the continuous wavelet transform. The 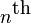$n^\textrm{th}$ Hermitian wavelet is defined as the 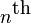$n^\textrm{th}$ derivative of a Gaussian distribution:

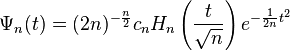
$\Psi_{n}(t)=(2n)^{-\frac{n}{2}}c_{n}H_{n}\left(\frac{t}{\sqrt{n}}\right)e^{-\frac{1}{2n}t^{2}}$

where 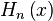$H_{n}\left({x}\right)$ denotes the 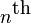$n^\textrm{th}$ Hermite polynomial.

The normalisation coefficient 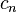$c_{n}$ is given by:

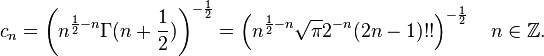
$c_{n} = \left(n^{\frac{1}{2}-n}\Gamma(n+\frac{1}{2})\right)^{-\frac{1}{2}} = \left(n^{\frac{1}{2}-n}\sqrt{\pi}2^{-n}(2n-1)!!\right)^{-\frac{1}{2}}\quad n\in\mathbb{Z}.$

The prefactor 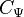$C_{\Psi}$ in the resolution of the identity of the continuous wavelet transform for this wavelet is given by:

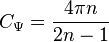
$C_{\Psi}=\frac{4\pi n}{2n-1}$

i.e. Hermitian wavelets are admissible for all positive $n$ .

In computer vision and image processing, Gaussian derivative operators of different orders are frequently used as a basis for expressing various types of visual operations; see scale space and N-jet.

Examples of Hermitian wavelets: Starting from a Gaussian function with 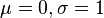$\mu=0, \sigma=1$ :

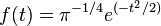
$f(t) = \pi^{-1/4}e^{(-t^2/2)}$

the first 3 derivatives read

\begin{align} f'(t) & = -\pi^{-1/4}te^{(-t^2/2)} \\ f''(t) & = \pi^{-1/4}(t^2 - 1)e^{(-t^2/2)}\\ f^{(3)}(t) & = \pi^{-1/4}(3t - t^3)e^{(-t^2/2)} \end{align}

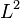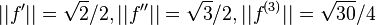
and their $L^2$ norms $||f'||=\sqrt{2}/2, ||f''||=\sqrt{3}/2, ||f^{(3)}||= \sqrt{30}/4$

So the wavelets which are the negative normalized derivatives are:

\begin{align} \Psi_{1}(t) &= \sqrt{2}\pi^{-1/4}te^{(-t^2/2)}\\ \Psi_{2}(t) &=\frac{2}{3}\sqrt{3}\pi^{-1/4}(1-t^2)e^{(-t^2/2)}\\ \Psi_{3}(t) &= \frac{2}{15}\sqrt{30}\pi^{-1/4}(t^3 - 3t)e^{(-t^2/2)} \end{align}

This article is issued from Wikipedia - version of the Sunday, July 20, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.