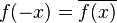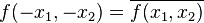Hermitian function

In mathematical analysis, a Hermitian function is a complex function with the property that its complex conjugate is equal to the original function with the variable changed in sign:

f(-x) = \overline{f(x)}

(where the overbar indicates the complex conjugate) for all $x$ in the domain of $f$ .

This definition extends also to functions of two or more variables, e.g., in the case that $f$ is a function of two variables it is Hermitian if

f(-x_1, -x_2) = \overline{f(x_1, x_2)}

for all pairs 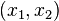$(x_1, x_2)$ in the domain of $f$ .

From this definition it follows immediately that: $f$ is a Hermitian function if and only if

the real part of $f$ is an even function, and
the imaginary part of $f$ is an odd function.

Motivation

Hermitian functions appear frequently in mathematics, physics, and signal processing. For example, the following two statements follow from basic properties of the Fourier transform:

The function $f$ is real-valued if and only if the Fourier transform of $f$ is Hermitian.

The function $f$ is Hermitian if and only if the Fourier transform of $f$ is real-valued.

Since the Fourier transform of a real signal is guaranteed to be Hermitian, it can be compressed using the Hermitian even/odd symmetry. This, for example, allows the discrete Fourier transform of a signal (which is in general complex) to be stored in the same space as the original real signal.

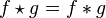If f is Hermitian, then $f \star g = f*g$ .

Where the $\star$ is cross-correlation, and $*$ is convolution.

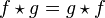If both f and g are Hermitian, then $f \star g = g \star f$ .

Hermitian function

Motivation

See also