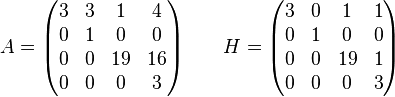Hermite normal form

In linear algebra, the Hermite normal form is an analogue of reduced echelon form for matrices over the integers Z.

Definition

Various authors may prefer to talk about Hermite Normal Form in either row-style or column-style. They are essentially the same up to transposition.

Row-style Hermite Normal Form

A matrix with integer entries is in (row) Hermite normal form (HNF) if

All nonzero rows (rows with at least one nonzero element) are above any rows of all zeroes (all zero rows, if any, are at the bottom of the matrix).
The leading coefficient (the first nonzero entry from the left, also called the pivot) of a nonzero row is always strictly to the right of the leading coefficient of the row above it; moreover, it is positive.
All entries in a column above a leading entry are nonnegative and strictly smaller than the leading entry.
All entries in a column below a leading entry are zeroes (implied by the first two criteria).

Nonsingular square matrices

In particular, a nonsingular square matrix with integer entries is in Hermite normal form (HNF) if

it is upper triangular,
its diagonal entries are positive,
in every column, the entries above the diagonal are non-negative and smaller than the entry on the diagonal.

Existence and uniqueness of the Hermite normal form

For every m×n matrix A with integer entries there is a unique m×n matrix H, in (HNF), with integer entries such that

H=UA with U ∈ GL_m(Z)

(i.e. U is unimodular).

Equivalently, H is the unique matrix in (HNF) with integer entries that can be obtained from A by means of a finite sequence of elementary row operations over Z (the only admissible row multiplications are by ±1).

Examples

The Hermite normal form of matrix A (on the left) is matrix H (on the right):

A=\begin{pmatrix} 3 & 3 & 1 & 4 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 19 & 16 \\ 0 & 0 & 0 & 3 \end{pmatrix} \qquad H=\begin{pmatrix} 3 & 0 & 1 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 &19 & 1\\ 0 & 0 & 0 & 3 \end{pmatrix}

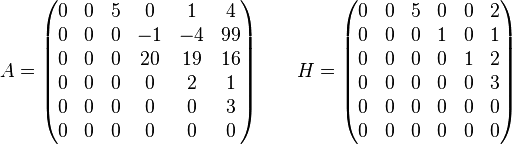
$A= \begin{pmatrix} 0&0&5 & 0 & 1 & 4 \\ 0&0&0 & -1 & -4 & 99 \\ 0&0&0 & 20 & 19 & 16 \\ 0&0&0 & 0 & 2 & 1\\ 0&0&0 & 0 & 0 & 3\\ 0&0&0 & 0 & 0 & 0 \end{pmatrix} \qquad H= \begin{pmatrix} 0& 0& 5& 0& 0& 2\\ 0& 0& 0& 1& 0& 1\\ 0& 0& 0& 0& 1& 2\\ 0& 0& 0& 0& 0& 3\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ \end{pmatrix}$

If A has only one row then either H = A or H = -A, depending on whether the single row of A has a positive or negative leading coefficient.

Alternative definitions

There are various versions of Hermite normal form in the literature, not equivalent to the above one. For instance —to distinguish this definition from the above one, we call this form (HNF')— an m×n matrix M = (m_ij) with integer entries is in (HNF') if there exists

r with 0 ≤ r ≤ n,
a strictly increasing function f: [r + 1, n] → [1, m],

such that the first r columns of M are zero, and for r + 1 ≤ j ≤ n

m_f(j)j > 0,
m_ij = 0 when i > f(j),
m_f(i)i > m_f(i)j ≥ 0 when i < f(j).

With this definition, for every m×n matrix B with integer entries there is a unique m×n matrix M, in (HNF'), with integer entries such that

M=BU with U ∈ GL_n(Z).

Some authors prefer using lower triangular matrices; suitable adjustments must be made to the rest of the definition.

References

Section 2.4.2 of Cohen, Henri (1993), A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics 138, Berlin, New York: Springer-Verlag, ISBN 978-3-540-55640-4, MR 1228206

This article is issued from Wikipedia - version of the Monday, February 01, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.