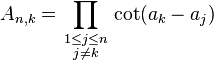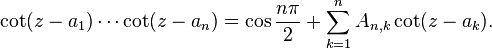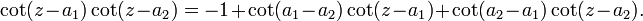Hermite's cotangent identity

Not to be confused with Hermite's identity, a statement about fractional parts of integer multiples of real numbers.

In mathematics, Hermite's cotangent identity is a trigonometric identity discovered by Charles Hermite.^[1] Suppose a₁, ..., a_n are complex numbers, no two of which differ by an integer multiple of $π$ . Let

A_{n,k} = \prod_{\begin{smallmatrix} 1 \le j \le n \\ j \neq k \end{smallmatrix}} \cot(a_k - a_j)

(in particular, A_1,1, being an empty product, is 1). Then

\cot(z - a_1)\cdots\cot(z - a_n) = \cos\frac{n\pi}{2} + \sum_{k=1}^n A_{n,k} \cot(z - a_k).

The simplest non-trivial example is the case n = 2:

\cot(z - a_1)\cot(z - a_2) = -1 + \cot(a_1 - a_2)\cot(z - a_1) + \cot(a_2 - a_1)\cot(z - a_2). \,

Notes and references

↑ Warren P. Johnson, "Trigonometric Identities à la Hermite", American Mathematical Monthly, volume 117, number 4, April 2010, pages 311–327

This article is issued from Wikipedia - version of the Saturday, February 06, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.