Hennessy–Milner logic

In computer science, Hennessy–Milner logic (HML) is a dynamic logic used to specify properties of a labeled transition system, a structure similar to an automaton. It was introduced in 1980 by Matthew Hennessy and Robin Milner in their paper 'On observing nondeterminism and concurrency' (ICALP).

Another variant of the HML involves the use of recursion to extend the expressibility of the logic, and is commonly referred to as 'Hennessy-Milner Logic with recursion'.^[1] Recursion is enabled with the use of maximum and minimum fixed points.

Syntax

A formula is defined by the following BNF grammar for L some set of actions:

That is, a formula can be

constant truth

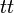
always true

constant false

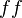
always false

formula conjunction

formula disjunction

formula 

for all L-derivatives, Φ must hold

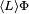formula 

for some L-derivative, Φ must hold

See also

• The modal μ-calculus extends HML with fixed point operators.
• Dynamic logic, a multimodal logic with infinitely many modalities.

References

• Colin P. Stirling (2001). Modal and temporal properties of processes. Springer. pp. 32–39. ISBN 978-0-387-98717-0. 
• Sören Holmström. 1988. Hennessy-Milner Logic with Recursion as a Specification Language, and a Refinement Calculus based on It. In Proceedings of the BCS-FACS Workshop on Specification and Verification of Concurrent Systems, Charles Rattray (Ed.). Springer-Verlag, London, UK, 294-330.

1. ↑ Holmström, Sören (1990). "Hennessy-Milner Logic with Recursion as a Specification Language, and a Refinement Calculus based on It". Proceedings of the BCS-FACS Workshop on Specification and Verification of Concurrent Systems: 294–330.