Helmholtz resonance

A brass, spherical Helmholtz resonator based on his original design, circa 1890-1900.

Helmholtz resonance is the phenomenon of air resonance in a cavity, such as when one blows across the top of an empty bottle. The name comes from a device created in the 1850s by Hermann von Helmholtz, the "Helmholtz resonator", which he used to identify the various frequencies or musical pitches present in music and other complex sounds.^[1]

Qualitative explanation

Helmholtz described in his 1862 book, "On the Sensations of Tone", an apparatus able to pick out specific frequencies from a complex sound. The Helmholtz resonator, as it is now called, consists of a rigid container of a known volume, nearly spherical in shape, with a small neck and hole in one end and a larger hole in the other end to admit the sound.

When the resonator's 'nipple' is placed inside one's ear, a specific frequency of the complex sound can be picked out and heard clearly. In Helmholtz’ book we read: When we “apply a resonator to the ear, most of the tones produced in the surrounding air will be considerably damped; but if the proper tone of the resonator is sounded, it brays into the ear most powerfully…. The proper tone of the resonator may even be sometimes heard cropping up in the whistling of the wind, the rattling of carriage wheels, the splashing of water.”

A set of varied size resonators was sold to be used as discrete acoustic filters for the spectral analysis of complex sounds. Picture: Resonator from Koenig's Acoustic Catalogue, 1889. Cost: 380 francs for a series of 14 resonators.

There is also an adjustable type, called a universal resonator, which consists of two cylinders, one inside the other, which can slide in or out to change the volume of the cavity over a continuous range. This type of resonator is in use in the Fourier analyzer, and is equivalent to tone variator in its function. <http://www.phys.cwru.edu/ccpi/Helmholtz_resonator.html> When air is forced into a cavity, the pressure inside increases. When the external force pushing the air into the cavity is removed, the higher-pressure air inside will flow out. Due to the inertia of the moving air the cavity will be left at a pressure slightly lower than the outside, causing air to be drawn back in. This process repeats, with the magnitude of the pressure oscillations increasing and decreasing asymptotically after the sound starts and stops.

The port (the neck of the chamber) is placed in the external meatus of the ear, allowing the experimenter to hear the sound and to determine its loudness. The resonant mass of air in the chamber is set in motion through the second hole, which is larger and doesn't have a neck.

A gastropod seashell can form a low Q Helmholtz resonator, resulting in the "sounds of the sea".

The term Helmholtz resonator is now more generally applied to include bottles from which sound is generated by blowing air across the mouth of the bottle. In this case the length and diameter of the bottle neck also contribute to the resonance frequency and its Q factor.

By one definition a Helmholtz resonator augments the amplitude of the vibratory motion of the enclosed air in a chamber by taking energy from sound waves passing in the surrounding air. In the other definition the sound waves are generated by a uniform stream of air flowing across the open top of an enclosed volume of air.

Quantitative explanation

It can be shown^[2] that the resonant angular frequency is given by:

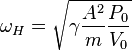\omega_{H} = \sqrt{\gamma\frac{A^2}{m} \frac{P_0}{V_0}}

(rad/s),

where:

$\gamma$ (gamma) is the adiabatic index or ratio of specific heats. This value is usually 1.4 for air and diatomic gases.
$A$ is the cross-sectional area of the neck;
$m$ is the mass in the neck;
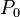$P_0$ is the static pressure in the cavity;
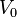$V_0$ is the static volume of the cavity.

For cylindrical or rectangular necks, we have

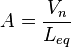A = \frac{V_n}{L_{eq}}

where:

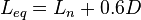$L_{eq}$ is the equivalent length of the neck with end correction, which can be calculated as : $L_{eq} = L_n + 0.6 D$ , where $L_n$ is the actual length of the neck and $D$ is the hydraulic diameter of the neck;^[3]
$V_n$ is the volume of air in the neck,

thus:

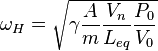\omega_{H} = \sqrt{\gamma\frac{A}{m} \frac{V_n}{L_{eq}} \frac{P_0}{V_0}}

From the definition of mass density (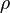 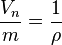${\rho}$ ): $\frac{V_n}{m} = \frac{1}{\rho}$ , thus:

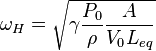\omega_{H} = \sqrt{\gamma\frac{P_0}{\rho} \frac{A}{V_0 L_{eq}}}

and

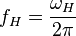f_H = \frac{\omega_H}{2\pi}

where:

f_H is the resonant frequency (Hz).

The speed of sound in a gas is given by:

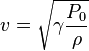v = \sqrt{\gamma\frac{P_0}{\rho}}

thus, the frequency of the resonance is:

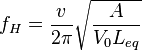f_{H} = \frac{v}{2\pi}\sqrt{\frac{A}{V_0 L_{eq}}}

The length of the neck appears in the denominator because the inertia of the air in the neck is proportional to the length. The volume of the cavity appears in the denominator because the spring constant of the air in the cavity is inversely proportional to its volume. The area of the neck matters for two reasons. Increasing the area of the neck increases the inertia of the air proportionately, but also decreases the velocity at which the air rushes in and out.

Depending on the exact shape of the hole, the relative thickness of the sheet with respect to the size of the hole and the size of the cavity, this formula can have limitations. More sophisticated formulae can still be derived analytically, with similar physical explanations (although some differences matter). See for example the book by F. Mechels.^[4] Furthermore, if the mean flow over the resonator is high (typically with a Mach number above 0.3), some corrections must be applied.

Applications

Helmholtz resonance finds application in internal combustion engines (see airbox), subwoofers and acoustics. Intake systems described as 'Helmholtz Systems' have been used in the Chrysler V10 engine built for both the Dodge Viper and the Ram pickup truck, and several of the Buell tube-frame series of motorcycles. In stringed instruments, such as the guitar and violin, the resonance curve of the instrument has the Helmholtz resonance as one of its peaks, along with other peaks coming from resonances of the vibration of the wood. An ocarina is essentially a Helmholtz resonator where the combined area of the opened finger holes determines the note played by the instrument.^[5] The West African djembe is a Helmholtz resonator with a small neck area, giving it a deep bass tone.

The theory of Helmholtz resonators is used in motorcycle and car exhausts to alter the sound of the exhaust note and for differences in power delivery by adding chambers to the exhaust. Exhaust resonators are also used to reduce potentially loud and obnoxious engine noise where the dimensions are calculated so that the waves reflected by the resonator help cancel out certain frequencies of sound in the exhaust.

In some two-stroke engines, a Helmholtz resonator is used to remove the need for a reed valve. A similar effect is also used in the exhaust system of most two-stroke engines, using a reflected pressure pulse to supercharge the cylinder (see Kadenacy effect.)

Helmholtz resonators are used in architectural acoustics to reduce undesirable low frequency sounds (standing waves, etc.) by building a resonator tuned to the problem frequency, thereby eliminating it.

Helmholtz resonators are also used to build acoustic liners for reducing the noise of aircraft engines, for example. These acoustic liners are made of two components:

a simple sheet of metal (or other material) perforated with little holes spaced out in a regular or irregular pattern; this is called a resistive sheet;
a series of so-called honeycomb cavities (holes with a honeycomb shape, but in fact only their volume matters).

Such acoustic liners are used in most of today's aircraft engines. The perforated sheet is usually visible from inside or outside the airplane; the honeycomb is just under it. The thickness of the perforated sheet is of importance, as shown above. Sometimes there are two layers of liners; they are then called "2-DOF liners" (DOF meaning Degrees Of Freedom), as opposed to "single DOF liners".

This effect might also be used to reduce skin friction drag on aircraft wings by 40%.^[6]

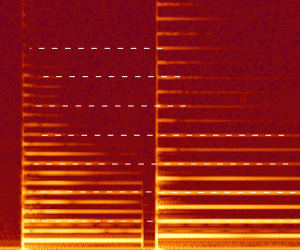
Helmholtz resonance sometimes occurs when a slightly open single car window makes a very loud sound, also called "side window buffeting".^[7]

Notes

↑ Helmholtz, Hermann von (1885), On the sensations of tone as a physiological basis for the theory of music, Second English Edition, translated by Alexander J. Ellis. London: Longmans, Green, and Co., p. 44. Retrieved 2010-10-12.
↑ Derivation of the equation for the resonant frequency of an Helmholtz resonator.
↑ End Correction at a Flue Pipe Mouth
↑ Formulas of Acoustics
↑ "Ocarina Physics - How Ocarinas Work". ocarinaforest.com. Retrieved 2012-12-31.
↑ Wings that waggle could cut aircraft emissions by 20%
↑ Why Do Slightly Opened Car Windows Make That Awful Sound?

Sources

Wikimedia Commons has media related to Helmholtz resonators.

Oxford Physics Teaching, History Archive, "Exhibit 3 - Helmholtz resonators" (archival photograph)
HyperPhysics Acoustic Laboratory
HyperPhysics Cavity Resonance
Beverage Bottles as Helmholtz ResonatorsScience Project Idea for Students
Helmholtz Resonance (web site on music acoustics)
Helmholtz's Sound Synthesiser on '120 years Of Electronic Music'

Acoustics

Engineering	Architectural acoustics Piano acoustics Reverberation Soundproofing Vibrating string string resonance	Spectrogram

Psychoacoustics	Bark scale Combination tone Equal-loudness contour Fletcher–Munson curves Mel scale Missing fundamental

Frequency Pitch	Beat Formant Fundamental frequency Frequency spectrum harmonic spectrum Harmonic series inharmonicity Overtone Resonance Subharmonic undertone series

Acousticians	John Backus Jens Blauert Ernst Chladni Hermann von Helmholtz Werner Meyer-Eppler Lord Rayleigh Joseph Sauveur D. Van Holliday Thomas Young

Related topics	Echo Infrasound Sound Ultrasound Mersenne's laws Musical acoustics piano Node

This article is issued from Wikipedia - version of the Sunday, December 06, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.