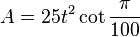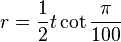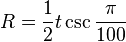Hectogon
| Regular hectogon | |
|---|---|
|
A regular hectogon | |
| Type | Regular polygon |
| Edges and vertices | 100 |
| Schläfli symbol | {100}, t{50}, tt{25} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D100), order 2×100 |
| Internal angle (degrees) | 176.4° |
| Dual polygon | self |
| Properties | convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a hectogon or hecatontagon[1][2] is a hundred-sided polygon or 100-gon.[3][4] The sum of any hectogon's interior angles is 17640 degrees.
Regular hectogon
A regular hectogon is represented by Schläfli symbol {100} and can be constructed as a truncated pentacontagon, t{50}, or a twice-truncated icosipentagon, tt{25}.
One interior angle in a regular hectogon is 1762⁄5°, meaning that one exterior angle would be 33⁄5°.
The area of a regular hectogon is (with t = edge length)
and its inradius is
The circumradius of a regular hectogon is
Because 100 = 22 × 52, the number of sides is neither a product of distinct Fermat primes nor a power of two. Thus the regular hectogon is not a constructible polygon.[5] Indeed, it is not even constructible with the use of neusis or an angle trisector, as the number of sides is neither a product of distinct Pierpont primes, nor a product of powers of two and three.[6]
Symmetry
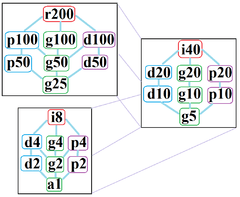
The regular hectogon has Dih100 dihedral symmetry, order 200, represented by 100 lines of reflection. Dih100 has 8 dihedral subgroups: (Dih50, Dih25), (Dih20, Dih10, Dih5), (Dih4, Dih2, and Dih1). It also has 9 more cyclic symmetries as subgroups: (Z100, Z50, Z25), (Z20, Z10, Z5), and (Z4, Z2, Z1), with Zn representing π/n radian rotational symmetry.
John Conway labels these lower symmetries with a letter and order of the symmetry follows the letter.[7] r200 represents full symmetry and a1 labels no symmetry. He gives d (diagonal) with mirror lines through vertices, p with mirror lines through edges (perpendicular), i with mirror lines through both vertices and edges, and g for rotational symmetry.
These lower symmetries allows degrees of freedom in defining irregular hectogons. Only the g100 subgroup has no degrees of freedom but can seen as directed edges.
Hectogram
A hectogram is an 100-sided star polygon. There are 19 regular forms[8] given by Schläfli symbols {100/3}, {100/7}, {100/9}, {100/11}, {100/13}, {100/17}, {100/19}, {100/21}, {100/23}, {100/27}, {100/29}, {100/31}, {100/33}, {100/37}, {100/39}, {100/41}, {100/43}, {100/47}, and {100/49}, as well as 30 regular star figures with the same vertex configuration.
| Picture |  {100/3} |
 {100/7} |
 {100/11} |
 {100/13} |
 {100/17} |
 {100/19} |
|---|---|---|---|---|---|---|
| Interior angle | 169.2° | 154.8° | 140.4° | 133.2° | 118.8° | 111.6° |
| Picture |  {100/21} |
 {100/23} |
 {100/27} |
 {100/29} |
 {100/31} |
 {100/37} |
| Interior angle | 104.4° | 97.2° | 82.8° | 75.6° | 68.4° | 46.8° |
| Picture |  {100/39} |
 {100/41} |
 {100/43} |
 {100/47} |
 {100/49} |
|
| Interior angle | 39.6° | 32.4° | 25.2° | 10.8° | 3.6° |
References
- ↑
- ↑
- ↑ Gorini, Catherine A. (2009), The Facts on File Geometry Handbook, Infobase Publishing, p. 110, ISBN 9781438109572.
- ↑ The New Elements of Mathematics: Algebra and Geometry by Charles Sanders Peirce (1976), p.298
- ↑ Constructible Polygon
- ↑ http://www.math.iastate.edu/thesisarchive/MSM/EekhoffMSMSS07.pdf
- ↑ The Symmetries of Things, Chapter 20
- ↑ 19 = 50 cases - 1 (convex) - 10 (multiples of 5) - 25 (multiples of 2)+ 5 (multiples of 2 and 5)
| ||||||||||||||||||||||||||