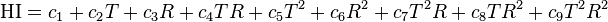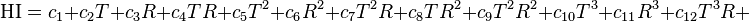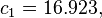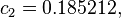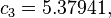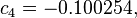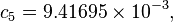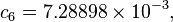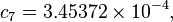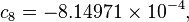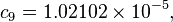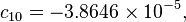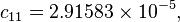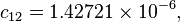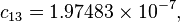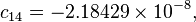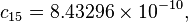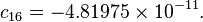Heat index

Humidity and hygrometry
Specific concepts
General concepts
Measures and Instruments

The heat index (HI) or humiture or humidex (not to be confused with the Canadian humidex) is an index that combines air temperature and relative humidity in an attempt to determine the human-perceived equivalent temperature—how hot it would feel if the humidity were some other value. The result is also known as the "felt air temperature" or "apparent temperature". For example, when the temperature is 32 °C (90 °F) with very high humidity, the heat index can be about 41 °C (106 °F).

The human body normally cools itself by perspiration, or sweating. Heat is removed from the body by evaporation of that sweat. However, high relative humidity reduces the evaporation rate. This results in a lower rate of heat removal from the body, hence the sensation of being overheated. This effect is subjective; its measurement has been based on subjective descriptions of how hot subjects feel for a given temperature and humidity. This results in a heat index that relates one combination of temperature and humidity to another.

History

The heat index was developed in 1978 by George Winterling as the "humiture" and was adopted by the USA's National Weather Service a year later.[1] It is derived from work carried out by Robert G. Steadman.[2][3] Like the wind chill index, the heat index contains assumptions about the human body mass and height, clothing, amount of physical activity, thickness of blood, sunlight and ultraviolet radiation exposure, and the wind speed. Significant deviations from these will result in heat index values which do not accurately reflect the perceived temperature.[4]

In Canada, the similar humidex is used in place of the heat index. While both the humidex and the heat index are calculated using dew point, the humidex uses a dew point of 45 °F (7 °C) as a base, whereas the heat index uses a dew point base of 57 °F (14 °C). Further, the heat index uses heat balance equations which account for many variables other than vapor pressure, which is used exclusively in the humidex calculation. A joint committee formed by the United States and Canada to resolve differences has since been disbanded .

The heat index is defined so as to equal the actual air temperature when the partial pressure of water vapor is equal to a baseline value of 1.6 kPa. At standard atmospheric pressure (101.325 kPa), this baseline corresponds to a dew point of 14 °C (57 °F) and a mixing ratio of 0.01 (10 g of water vapor per kilogram of dry air).[2] This corresponds to an air temperature of 25 °C (77 °F) and relative humidity of 50% in the sea-level psychrometric chart.

A given value of relative humidity causes larger increases in the heat index at higher temperatures. For example, at approximately 27 °C (81 °F), the heat index will agree with the actual temperature if the relative humidity is 45%, but at 43 °C (109 °F), any relative-humidity reading above 18% will make the heat index higher than 43 °C.

It has been suggested that the equation described is valid only if the temperature is 27 °C (80 °F) or more, and the relative humidity is 40% or more.[5] However, a recent analysis by iWeatherNet found the assumption to be erroneous given that the heat index/relative humidity relationship and the corresponding equilibrium temperature (the point at which the air temperature and the heat index are equal) are nonlinear. The heat index and humidex figures are based on temperature measurements taken in the shade and not the sun, so extra care must be taken while in the sun. The heat index also does not factor in the effects of wind, which lowers the apparent temperature, unless the air is above body temperature.

Sometimes the heat index and the wind chill are denoted collectively by the single term "apparent temperature", "relative outdoor temperature", or "feels like".

Meteorological considerations

Outdoors in open conditions, as the relative humidity increases, first haze and ultimately a thicker cloud cover develops, reducing the amount of direct sunlight reaching the surface. Thus, there is an inverse relationship between maximum potential temperature and maximum potential relative humidity. Because of this factor, it was once believed that the highest heat index reading actually attainable anywhere on Earth is approximately 71 °C (160 °F). However, in Dhahran, Saudi Arabia on July 8, 2003, the dew point was 35 °C (95 °F) while the temperature was 42 °C (108 °F), resulting in a heat index of 78 °C (172 °F).

Table of values

This table is from the U.S. National Oceanic and Atmospheric Administration.

NOAA national weather service: heat index
  Temperature
80 °F (27 °C) 82 °F (28 °C) 84 °F (29 °C) 86 °F (30 °C) 88 °F (31 °C) 90 °F (32 °C) 92 °F (33 °C) 94 °F (34 °C) 96 °F (36 °C) 98 °F (37 °C) 100 °F (38 °C) 102 °F (39 °C) 104 °F (40 °C) 106 °F (41 °C) 108 °F (42 °C) 110 °F (43 °C)
Relative humidity (%)
40 80 °F (27 °C) 81 °F (27 °C) 83 °F (28 °C) 85 °F (29 °C) 88 °F (31 °C) 91 °F (33 °C) 94 °F (34 °C) 97 °F (36 °C) 101 °F (38 °C) 105 °F (41 °C) 109 °F (43 °C) 114 °F (46 °C) 119 °F (48 °C) 124 °F (51 °C) 130 °F (54 °C) 136 °F (58 °C)
45 80 °F (27 °C) 82 °F (28 °C) 84 °F (29 °C) 87 °F (31 °C) 89 °F (32 °C) 93 °F (34 °C) 96 °F (36 °C) 100 °F (38 °C) 104 °F (40 °C) 109 °F (43 °C) 114 °F (46 °C) 119 °F (48 °C) 124 °F (51 °C) 130 °F (54 °C) 137 °F (58 °C)
50 81 °F (27 °C) 83 °F (28 °C) 85 °F (29 °C) 88 °F (31 °C) 91 °F (33 °C) 95 °F (35 °C) 99 °F (37 °C) 103 °F (39 °C) 108 °F (42 °C) 113 °F (45 °C) 118 °F (48 °C) 124 °F (51 °C) 131 °F (55 °C) 137 °F (58 °C)
55 81 °F (27 °C) 84 °F (29 °C) 86 °F (30 °C) 89 °F (32 °C) 93 °F (34 °C) 97 °F (36 °C) 101 °F (38 °C) 106 °F (41 °C) 112 °F (44 °C) 117 °F (47 °C) 124 °F (51 °C) 130 °F (54 °C) 137 °F (58 °C)
60 82 °F (28 °C) 84 °F (29 °C) 88 °F (31 °C) 91 °F (33 °C) 95 °F (35 °C) 100 °F (38 °C) 105 °F (41 °C) 110 °F (43 °C) 116 °F (47 °C) 123 °F (51 °C) 129 °F (54 °C) 137 °F (58 °C)
65 82 °F (28 °C) 85 °F (29 °C) 89 °F (32 °C) 93 °F (34 °C) 98 °F (37 °C) 103 °F (39 °C) 108 °F (42 °C) 114 °F (46 °C) 121 °F (49 °C) 128 °F (53 °C) 136 °F (58 °C)
70 83 °F (28 °C) 86 °F (30 °C) 90 °F (32 °C) 95 °F (35 °C) 100 °F (38 °C) 105 °F (41 °C) 112 °F (44 °C) 119 °F (48 °C) 126 °F (52 °C) 134 °F (57 °C)
75 84 °F (29 °C) 88 °F (31 °C) 92 °F (33 °C) 97 °F (36 °C) 103 °F (39 °C) 109 °F (43 °C) 116 °F (47 °C) 124 °F (51 °C) 132 °F (56 °C)
80 84 °F (29 °C) 89 °F (32 °C) 94 °F (34 °C) 100 °F (38 °C) 106 °F (41 °C) 113 °F (45 °C) 121 °F (49 °C) 129 °F (54 °C)
85 85 °F (29 °C) 90 °F (32 °C) 96 °F (36 °C) 102 °F (39 °C) 110 °F (43 °C) 117 °F (47 °C) 126 °F (52 °C) 135 °F (57 °C)
90 86 °F (30 °C) 91 °F (33 °C) 98 °F (37 °C) 105 °F (41 °C) 113 °F (45 °C) 122 °F (50 °C) 131 °F (55 °C)
95 86 °F (30 °C) 93 °F (34 °C) 100 °F (38 °C) 108 °F (42 °C) 117 °F (47 °C) 127 °F (53 °C)
100 87 °F (31 °C) 95 °F (35 °C) 103 °F (39 °C) 112 °F (44 °C) 121 °F (49 °C) 132 °F (56 °C)
  Caution
  Extreme caution
  Danger
  Extreme danger

For example, if the air temperature is 96 °F / 36 °C and the relative humidity is 65%, the heat index is 121 °F / 49 °C.

Effects of the heat index (shade values)

Celsius Fahrenheit Notes
27–32 °C 80–91 °F Caution: fatigue is possible with prolonged exposure and activity. Continuing activity could result in heat cramps.
32–41 °C 90–105 °F Extreme caution: heat cramps and heat exhaustion are possible. Continuing activity could result in heat stroke.
41–54 °C 105–130 °F Danger: heat cramps and heat exhaustion are likely; heat stroke is probable with continued activity.
over 54 °C over 130 °F Extreme danger: heat stroke is imminent.

Exposure to full sunshine can increase heat index values by up to 8 °C (14 °F).[6]

Formula

The formula below approximates the heat index in degrees Fahrenheit, to within ±1.3 °F. It is the result of a multivariate fit (temperature equal to or greater than 80 °F and relative humidity equal to or greater than 40%) to a model of the human body.[7][8] This equation reproduces the above NOAA National Weather Service table (except the values at 90 °F & 45%/70% relative humidity vary unrounded by less than -1/+1, respectively).

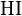\mathrm{HI} = c_1 + c_2 T + c_3 R + c_4 T R + c_5 T^2 + c_6 R^2 + c_7 T^2R + c_8 T R^2 + c_9 T^2 R^2\ \,

where

\mathrm{HI}\,\! = heat index (in degrees Fahrenheit)
T\,\! = ambient dry-bulb temperature (in degrees Fahrenheit)
R\,\! = relative humidity (percentage value between 0 and 100)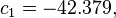
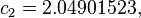
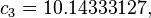
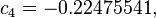
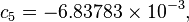
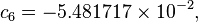
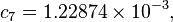
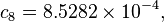
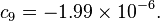
c_1 = -42.379, \,\! c_2 = 2.04901523, \,\! c_3 = 10.14333127,\,\! c_4 = -0.22475541, \,\! c_5 = -6.83783 \times 10^{-3},\,\! c_6 = -5.481717 \times 10^{-2},\,\! c_7 = 1.22874 \times 10^{-3}, \,\! c_8 = 8.5282 \times 10^{-4}, \,\! c_9 = -1.99 \times 10^{-6}.\,\!

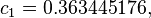
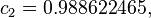
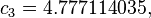
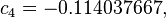
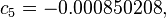
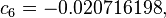
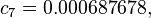
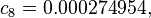
An alternative set of constants for this equation that is within 3 degrees of the NWS master table for all humidities from 0 to 80% and all temperatures between 70 and 115 °F and all heat indexes < 150 °F is: c_1 = 0.363445176, \,\! c_2 = 0.988622465, \,\! c_3 = 4.777114035, \,\! c_4 = -0.114037667, \,\! c_5 = -0.000850208, \,\! c_6 = -0.020716198, \,\! c_7 = 0.000687678, \,\! c_8 = 0.000274954, \,\! c_9 = 0 \,\! (c_9 \,\! unused).

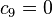
A further alternate is this:[9]

\mathrm{HI} = c_1 + c_2 T + c_3 R + c_4 T R + c_5 T^2 + c_6 R^2 + c_7 T^2 R + c_8 T R^2 + c_9 T^2 R^2 + c_{10} T^3 + c_{11} R^3 + c_{12} T^3 R +

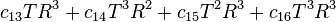
c_{13} T R^3 + c_{14} T^3 R^2 + c_{15} T^2 R^3 + c_{16} T^3 R^3\ \,

where

c_1 = 16.923, \,\! c_2 = 0.185212, \,\! c_3 = 5.37941,\,\! c_4 = -0.100254, \,\! c_5 = 9.41695 \times 10^{-3},\,\! c_6 = 7.28898 \times 10^{-3},\,\! c_7 = 3.45372\times 10^{-4}, \,\! c_8 = -8.14971 \times 10^{-4}, \,\! c_9 = 1.02102 \times 10^{-5},\,\! c_{10} = -3.8646 \times 10^{-5},\,\! c_{11} = 2.91583 \times 10^{-5},\,\! c_{12} = 1.42721 \times 10^{-6},\,\! c_{13} = 1.97483 \times 10^{-7},\,\! c_{14} = -2.18429 \times 10^{-8},\,\! c_{15} = 8.43296 \times 10^{-10},\,\! c_{16} = -4.81975 \times 10^{-11}.\,\!

For example, using this last formula, with temperature 90 °F (32 °C) and relative humidity (RH) of 85%, the result would be: Heat index for 90 °F, RH 85% = 114.9.

See also

References

  1. ↑ George Winterling: A Lifelong Passion For Weather WJXT, April 23, 2009
  2. 1 2 The Assessment of Sultriness. Part I: A Temperature-Humidity Index Based on Human Physiology and Clothing Science, R. G. Steadman, Journal of Applied Meteorology, July 1979, Vol 18 No7, pp861–873 doi:10.1175/1520-0450(1979)018<0861:TAOSPI>2.0.CO;2
  3. ↑ The Assessment of Sultriness. Part II: Effects of Wind, Extra Radiation and Barometric Pressure on Apparent Temperature, R. G. Steadman, Journal of Applied Meteorology, July 1979, Vol 18 No7, pp874–885
  4. ↑ How do they figure the heat index? - By Daniel Engber - Slate Magazine
  5. ↑ Heat Index Campbell Scientific Inc. (PDF file), CampbellSci.com.
  6. ↑ Heat Index on the website of the Pueblo, CO United States National Weather Service.
  7. ↑ Lans P. Rothfusz. "The Heat Index 'Equation' (or, More Than You Ever Wanted to Know About Heat Index)", Scientific Services Division (NWS Southern Region Headquarters), 1 July 1990
  8. ↑ R.G. Steadman, 1979. "The assessment of sultriness. Part I: A temperature-humidity index based on human physiology and clothing science," J. Appl. Meteor., 18, 861-873
  9. ↑ Stull, Richard (2000). Meteorology for Scientists and Engineers, Second Edition. Brooks/Cole. p. 60. ISBN 9780534372149.

External links

This article is issued from Wikipedia - version of the Thursday, February 11, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.