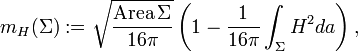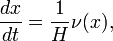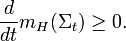Hawking energy

The Hawking energy or Hawking mass is one of the possible definitions of mass in general relativity. It is a measure of the bending of ingoing and outgoing rays of light that are orthogonal to a 2-sphere surrounding the region of space whose mass is to be defined.

Definition

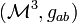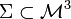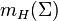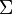Let (\mathcal{M}^3, g_{ab}) be a 3-dimensional sub-manifold of a relativistic spacetime, and let \Sigma \subset \mathcal{M}^3 be a closed 2-surface. Then the Hawking mass m_H(\Sigma) of \Sigma is defined[1] to be

m_H(\Sigma) := \sqrt{\frac{\text{Area}\,\Sigma}{16\pi}}\left( 1 - \frac{1}{16\pi}\int_\Sigma H^2 da \right),

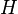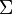where H is the mean curvature of \Sigma.

Properties

In the Schwarzschild metric, the Hawking mass of any sphere S_r about the central mass is equal to the value m of the central mass.

A result of Geroch[2] implies that Hawking mass satisfies an important monotonicity condition. Namely, if 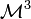\mathcal{M}^3 has nonnegative scalar curvature, then the Hawking mass of 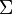\Sigma is non-decreasing as the surface 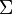\Sigma flows outward at a speed equal to the inverse of the mean curvature. In particular, if 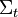\Sigma_t is a family of connected surfaces evolving according to

\frac{dx}{dt} = \frac{1}{H}\nu(x),

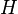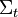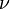where H is the mean curvature of \Sigma_t and \nu is the unit vector opposite of the mean curvature direction, then

\frac{d}{dt}m_H(\Sigma_t) \geq 0.

Said otherwise, Hawking mass is increasing for the inverse mean curvature flow.[3]

Hawking mass is not necessarily positive. However, it is asymptotic to the ADM[4] or the Bondi mass, depending on whether the surface is asymptotic to spatial infinity or null infinity.[5]

See also

References

  1. ↑ Page 21 of Schoen, Richard, 2005, "Mean Curvature in Riemannian Geometry and General Relativity," in Global Theory of Minimal Surfaces: Proceedings of the Clay Mathematics Institute 2001 Summer School, David Hoffman (Ed.), p.113-136.
  2. ↑ Geroch, Robert. 1973. "Energy Extraction." doi:10.1111/j.1749-6632.1973.tb41445.x.
  3. ↑ Lemma 9.6 of Schoen (2005).
  4. ↑ Section 4 of Yuguang Shi, Guofang Wang and Jie Wu (2008), "On the behavior of quasi-local mass at the infinity along nearly round surfaces".
  5. ↑ Section 2 of Shing Tung Yau (2002), "Some progress in classical general relativity," Geometry and Nonlinear Partial Differential Equations, Volume 29.
This article is issued from Wikipedia - version of the Sunday, July 26, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.