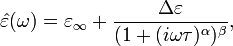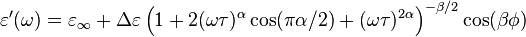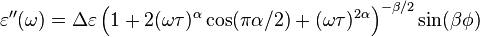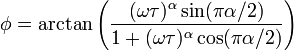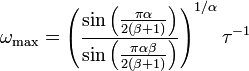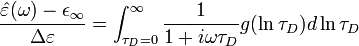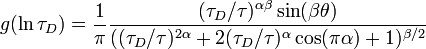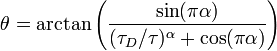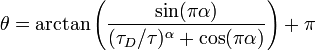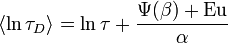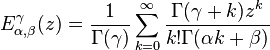Havriliak–Negami relaxation

Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model, accounting for the asymmetry and broadness of the dielectric dispersion curve. The model was first used to describe the dielectric relaxation of some polymers,^[1] by adding two exponential parameters to the Debye equation:

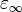\hat{\varepsilon}(\omega) = \varepsilon_{\infty} + \frac{\Delta\varepsilon}{(1+(i\omega\tau)^{\alpha})^{\beta}},

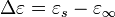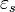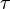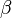where $\varepsilon_{\infty}$ is the permittivity at the high frequency limit, $\Delta\varepsilon = \varepsilon_{s}-\varepsilon_{\infty}$ where $\varepsilon_{s}$ is the static, low frequency permittivity, and $\tau$ is the characteristic relaxation time of the medium. The exponents $\alpha$ and $\beta$ describe the asymmetry and broadness of the corresponding spectra.

Depending on application, the Fourier transform of the stretched exponential function can be a viable alternative that has one parameter less.

For $\beta = 1$ the Havriliak–Negami equation reduces to the Cole–Cole equation, for $\alpha=1$ to the Cole–Davidson equation.

Mathematical properties

Real and imaginary parts

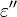The storage part $\varepsilon'$ and the loss part $\varepsilon''$ of the permittivity (here: 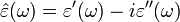$\hat{\varepsilon}(\omega) = \varepsilon'(\omega) - i \varepsilon''(\omega)$ ) can be calculated as

\varepsilon'(\omega) = \varepsilon_{\infty} + \Delta\varepsilon\left( 1 + 2 (\omega\tau)^\alpha \cos (\pi\alpha/2) + (\omega\tau)^{2\alpha} \right)^{-\beta/2} \cos (\beta\phi)

and

\varepsilon''(\omega) = \Delta\varepsilon\left( 1 + 2 (\omega\tau)^\alpha \cos (\pi\alpha/2) + (\omega\tau)^{2\alpha} \right)^{-\beta/2} \sin (\beta\phi)

with

\phi = \arctan \left( { (\omega\tau)^\alpha \sin(\pi\alpha/2) \over 1 + (\omega\tau)^\alpha \cos(\pi\alpha/2) } \right)

Loss peak

The maximum of the loss part lies at

\omega_{\rm max} = \left( { \sin \left( { \pi\alpha \over 2 ( \beta +1 ) } \right) \over \sin \left( { \pi\alpha\beta \over 2 ( \beta +1 ) } \right) } \right) ^ {1/\alpha} \tau^{-1}

Superposition of Lorentzians

The Havriliak–Negami relaxation can be expressed as a superposition of individual Debye relaxations

{ \hat{\varepsilon}(\omega) - \epsilon_\infty \over \Delta\varepsilon } = \int_{\tau_D=0}^\infty { 1 \over 1 + i \omega \tau_D } g( \ln \tau_D ) d \ln \tau_D

with the distribution function

g ( \ln \tau_D ) = { 1 \over \pi } { ( \tau_D / \tau )^{\alpha\beta} \sin (\beta\theta) \over ( ( \tau_D / \tau )^{2\alpha} + 2 ( \tau_D / \tau )^{\alpha} \cos (\pi\alpha) + 1 )^{\beta/2} }

where

\theta = \arctan \left( { \sin (\pi\alpha) \over ( \tau_D / \tau )^{\alpha} + \cos (\pi\alpha) } \right)

if the argument of the arctangent is positive, else^[2]

\theta = \arctan \left( { \sin (\pi\alpha) \over ( \tau_D / \tau )^{\alpha} + \cos (\pi\alpha) } \right) + \pi

Logarithmic moments

The first logarithmic moment of this distribution, the average logarithmic relaxation time is

\langle \ln\tau_D \rangle = \ln\tau + { \Psi(\beta) + {\rm Eu} \over \alpha }

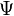where $\Psi$ is the digamma function and 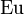${\rm Eu}$ the Euler constant.^[3]

Inverse Fourier transform

The inverse Fourier transform of the Havriliak-Negami function (the corresponding time-domain relaxation function) can be numerically calculated.^[4] It can be shown that the series expansions involved are special cases of the Fox-Wright function.^[5] In particular, in the time-domain the corresponding of 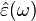$\hat{\varepsilon}(\omega)$ can be represented as

Failed to parse (unknown function "\apha"): X(t) = \varepsilon_{\infty} \delta(t) + \frac{\Delta\varepsilon}{\tau} \left( \frac{t}{\tau}\right)^{\alpha\beta-1} E_{\alpha,\alpha\beta}^{\beta}(-(t/\tau)^{\apha}) ,

where $\delta(t)$ is the Dirac delta function and

E_{\alpha,\beta}^{\gamma}(z) = \frac{1}{\Gamma(\gamma)} \sum_{k=0}^{\infty} \frac{\Gamma(\gamma+k) z^{k}}{k! \Gamma(\alpha k + \beta)}

is a special instance of the Fox-Wright function and, precisely, it is the three parameters Mittag-Leffler function^[6] also known as the Prabhakar function. The function 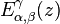$E_{\alpha,\beta}^{\gamma}(z)$ can be numerically evaluated, for instance, by means of a Matlab code .^[7]

References

↑ Havriliak, S.; Negami, S. (1967). "A complex plane representation of dielectric and mechanical relaxation processes in some polymers". Polymer 8: 161–210. doi:10.1016/0032-3861(67)90021-3.
↑ Zorn, R. (1999). "Applicability of Distribution Functions for the Havriliak–Negami Spectral Function". Journal of Polymer Science Part B 37 (10): 1043–1044. Bibcode:1999JPoSB..37.1043Z. doi:10.1002/(SICI)1099-0488(19990515)37:10<1043::AID-POLB9>3.3.CO;2-8.
↑ Zorn, R. (2002). "Logarithmic moments of relaxation time distributions". Journal of Chemical Physics 116 (8): 3204–3209. Bibcode:2002JChPh.116.3204Z. doi:10.1063/1.1446035.
↑ Schönhals, A. (1991). "Fast calculation of the time dependent dielectric permittivity for the Havriliak-Negami function". Acta Polymerica 42: 149–151. line feed character in |title= at position 63 (help)
↑ Hilfer, J. (2002). "H-function representations for stretched exponential relaxation and non-Debye susceptibilities in glassy systems". Physical Review E 65: 061510. Bibcode:2002PhRvE..65f1510H. doi:10.1103/physreve.65.061510.
↑ Gorenflo, Rudolf; Kilbas, Anatoly A.; Mainardi, Francesco; Rogosin, Sergei V. (2014). Springer, ed. Mittag-Leffler Functions, Related Topics and Applications. ISBN 978-3-662-43929-6.
↑ Garrappa, Roberto. "The Mittag-Leffler function". Retrieved 3 November 2014.