Havel–Hakimi algorithm
The Havel–Hakimi algorithm is an algorithm in graph theory solving the graph realization problem, i.e. the question if there exists for a finite list of nonnegative integers a simple graph such that its degree sequence is exactly this list. For a positive answer the list of integers is called graphic. The algorithm constructs a special solution if one exists or proves that one cannot find a positive answer. This construction is based on a recursive algorithm. The algorithm was published by Havel (1955), and later by Hakimi (1962).
The algorithm
The algorithm is based on the following theorem.
Let 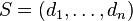 be a finite list of nonnegative integers that is nonincreasing. List
be a finite list of nonnegative integers that is nonincreasing. List 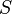 is graphic if and only if the finite list
is graphic if and only if the finite list 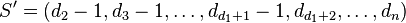 has nonnegative integers and is graphic.
has nonnegative integers and is graphic.
Is the given list 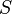 graphic then the theorem will be applied at most
graphic then the theorem will be applied at most  times setting in each further step
times setting in each further step 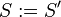 . Note that it can be necessary to sort this list again. This process ends when the whole list
. Note that it can be necessary to sort this list again. This process ends when the whole list 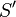 consists of zeros. In each step of the algorithm one constructs the edges of a graph with vertices
consists of zeros. In each step of the algorithm one constructs the edges of a graph with vertices 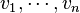 , i.e. if it is possible to reduce the list
, i.e. if it is possible to reduce the list 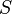 to
to 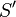 , then we add edges
, then we add edges 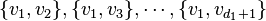 . When the list
. When the list 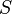 cannot be reduced to a list
cannot be reduced to a list 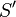 of nonnegative integers in any step of this approach, the theorem proves that the list
of nonnegative integers in any step of this approach, the theorem proves that the list 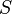 from the beginning is not graphic.
from the beginning is not graphic.
See also
References
- Havel, Václav (1955), "A remark on the existence of finite graphs", Časopis pro pěstování matematiky (in Czech) 80: 477–480
- Hakimi, S. L. (1962), "On realizability of a set of integers as degrees of the vertices of a linear graph. I", Journal of the Society for Industrial and Applied Mathematics 10: 496–506, MR 0148049.