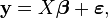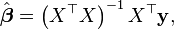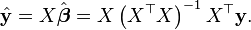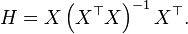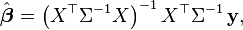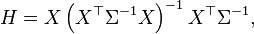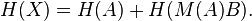Hat matrix
In statistics, the hat matrix, H, sometimes also called the influence matrix[1] or projection matrix, maps the vector of response values (dependent variable values) to the vector of fitted values (or predicted values). It describes the influence each response value has on each fitted value.[2][3] The diagonal elements of the hat matrix are the leverages, which describe the influence each response value has on the fitted value for that same observation.
If the vector of response values is denoted by y and the vector of fitted values by ŷ,
As ŷ is usually pronounced "y-hat", the hat matrix is so named as it "puts a hat on y". The formula for the vector of residuals r can also be expressed compactly using the hat matrix:
Moreover, the element in the ith row and jth column of H is equal to the covariance between the jth response value and the ith fitted value, divided by the variance of the former:
The covariance matrix of the residuals is therefore, by error propagation, equal to 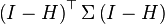 , where Σ is the covariance matrix of the error vector (and by extension, the response vector as well). For the case of linear models with independent and identically distributed errors in which Σ = σ2I, this reduces to (I − H)σ2.[2]
, where Σ is the covariance matrix of the error vector (and by extension, the response vector as well). For the case of linear models with independent and identically distributed errors in which Σ = σ2I, this reduces to (I − H)σ2.[2]
Many types of models and techniques are subject to this formulation. A few examples are:
- Linear model / linear least squares
- Smoothing splines
- Regression splines
- Local regression
- Kernel regression
- Linear filtering
Linear model
Suppose that we wish to estimate a linear model using linear least squares. The model can be written as
where X is a matrix of explanatory variables (the design matrix), β is a vector of unknown parameters to be estimated, and ε is the error vector.
Solution with unit weights and uncorrelated errors
When the weights for each observation are identical and the errors are uncorrelated, the estimated parameters are
so the fitted values are
Therefore the hat matrix is given by
The hat matrix has a number of useful algebraic properties.[4][5] In the language of linear algebra, the hat matrix is the orthogonal projection onto the column space of the design matrix X.[3](Note that 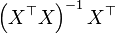 is the pseudoinverse of X.)
is the pseudoinverse of X.)
Some facts of the hat matrix in this setting are summarized as follows:[3]
-
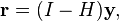 and
and 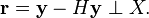
- H is symmetric, and so is I - H.
- H is idempotent:
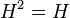 , and so is I - H.
, and so is I - H. - X is invariant under H :
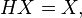 hence
hence 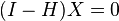 .
. -
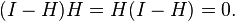
The hat matrix corresponding to a linear model is symmetric and idempotent, that is, 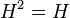 . However, this is not always the case; in locally weighted scatterplot smoothing (LOESS), for example, the hat matrix is in general neither symmetric nor idempotent.
. However, this is not always the case; in locally weighted scatterplot smoothing (LOESS), for example, the hat matrix is in general neither symmetric nor idempotent.
For linear models, the trace of the hat matrix is equal to the rank of X, which is the number of independent parameters of the linear model. For other models such as LOESS that are still linear in the observations y, the hat matrix can be used to define the effective degrees of freedom of the model.
Practical applications of the hat matrix in regression analysis include leverage and Cook's distance, which are concerned with identifying observations which have a large effect on the results of a regression.
More generally
Non-identical weights and/or correlated errors
The above may be generalized to the cases where the weights are not identical and/or the errors are correlated. Suppose that the covariance matrix of the errors is Σ. Then since
the hat matrix is thus
and again it may be seen that H2 = H, though now it is no longer symmetric.
Blockwise formula
Suppose the design matrix  can be decomposed by columns as
can be decomposed by columns as ![X= [A, B]](../I/m/a7c85836140c610b3d225eb8225d80da.png) .
Define the hat operator as
.
Define the hat operator as 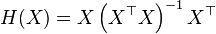 . Similarly, define the residual operator as
. Similarly, define the residual operator as 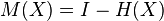 .
Then the hat matrix can be decomposed as follows:
.
Then the hat matrix can be decomposed as follows:
There are a number of applications of such a partitioning. The classical application has  a column of all ones, which allows one to analyze the effects of adding an intercept term to a regression. Another use is in the fixed effects model, where
a column of all ones, which allows one to analyze the effects of adding an intercept term to a regression. Another use is in the fixed effects model, where  is a large sparse matrix of the dummy variables for the fixed effect terms. One can use this partition to compute the hat matrix of
is a large sparse matrix of the dummy variables for the fixed effect terms. One can use this partition to compute the hat matrix of  without explicitly forming the matrix
without explicitly forming the matrix  , which might be too large to fit into computer memory.
, which might be too large to fit into computer memory.
See also
References
- ↑ Data Assimilation: Observation influence diagnostic of a data assimilation system
- 1 2 Hoaglin, David C.; Welsch, Roy E. (February 1978), "The Hat Matrix in Regression and ANOVA", The American Statistician 32 (1): 17–22, doi:10.2307/2683469, JSTOR 2683469
- 1 2 3 David A. Freedman (2009). Statistical Models: Theory and Practice. Cambridge University Press.
- ↑ Gans, P. (1992) Data Fitting in the Chemical Sciences,, Wiley. ISBN 978-0-471-93412-7
- ↑ Draper, N.R., Smith, H. (1998) Applied Regression Analysis, Wiley. ISBN 0-471-17082-8
- ↑ Rao, C. Radhakrishna; Toutenburg, Shalabh, Heumann (2008). Linear Models and Generalizations (3rd ed.). Berlin: Springer. p. 323. ISBN 978-3-540-74226-5. Cite uses deprecated parameter
|coauthors=(help)
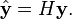
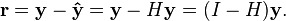
![\begin{align}
h_{ij} = \operatorname{cov}[\hat{y}_i, y_j] / \operatorname{var}[y_j]
\end{align}](../I/m/f6556d91dee3b6825ad008f788e211f2.png)